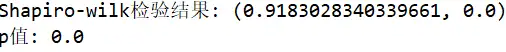Apple股票的收益和风险分析（1980---2019）

作者：三青时间：2023-05-10 阅读数：人阅读

股票的收益率及其分布，接着计算指示风险的统计量：方差、偏度和峰度，最后检验了收益分布的正态性。

一、股票的收益

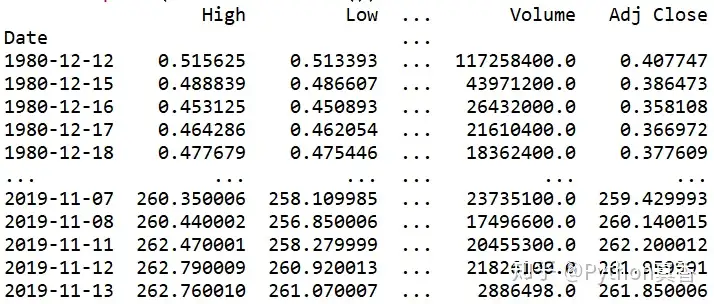
导入CSV时序数据并制作图表

import datetime import pandas as pd import pandas_datareader.data as web start = datetime.datetime(1980, 1, 1) end = datetime.date.today() df = web.DataReader(AAPL, yahoo, start, end) print(df.head(1000000)) df.to_csv(rE:\stock\apple.csv,index=True) StockPrices = pd.read_csv(rE:\stock\apple.csv,parse_dates=[Date], index_col=Date) #将数据按日期这一列排序（保证后续计算收益率的正确性） StockPrices = StockPrices.sort_values(by=Date) print(StockPrices.head())

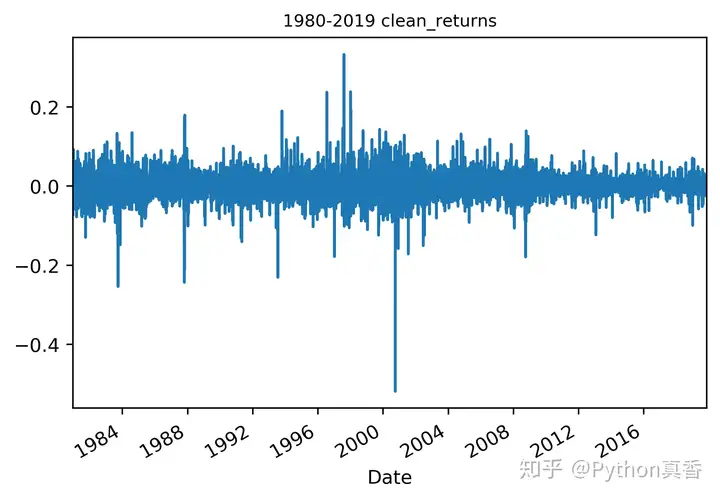
#1.计算收益率 #增加一列"Returns，存储每日的收益率 StockPrices[Return] = StockPrices[Adj Close].pct_change() #检查前5行数据 print(StockPrices.head()) #删除缺失值 clean_returns = StockPrices[Return].dropna() #绘制每日收益随时间变化的图 #导入matplotlib绘图包中的pyplot模块 import matplotlib.pyplot as plt clean_returns.plot() plt.title(1980-2019 clean_returns,fontsize=9) plt.savefig(E:\stock\收益率,dpi=400,bbox_inches=tight)#输出图表存入此地址中 plt.show()

#2.收益的均值

#导入numpy包

import numpy as np

#计算股票的日均平均值

mean_return_daily = np.mean(clean_returns)

print("日平均收益:",mean_return_daily)

#将日收益率转换为年化收益率

#计算平均年化收益

mean_return_annualized = ((1 + mean_return_daily)**252) - 1

print("平均年化收益:",mean_return_annualized)

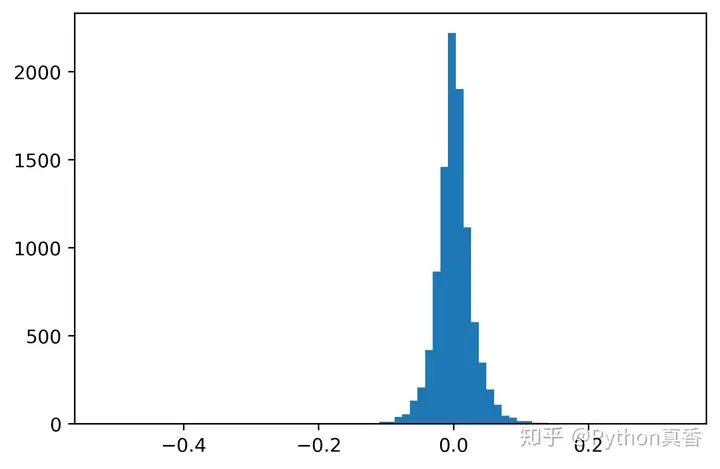
#3收益的分布 #绘制直方图 plt.hist(clean_returns, bins=75) plt.savefig(E:\stock\收益直方图,dpi=400,bbox_inches=tight) plt.show()

是正态分布？？？（后面我将围绕这个问题展开，因为金融市场的风险是对不确定性的度量，反应在收益的波动上。如果从长期看，股票收益符合正态分布，即股票的收益一定紧靠在平均收益旁边，那么是不是意味着：股票有风险，投资需谨慎，是一句空话？）

二、风险的衡量

金融市场的风险是对不确定性的度量，反应在收益的波动上。一般可用以下统计量来表示：

方差或标准差偏度峰度

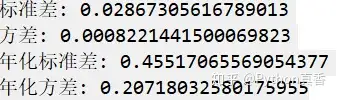
#计算标准差 sigma_daily = np.std(clean_returns) print("标准差:",sigma_daily) #计算方差 variance_daily = sigma_daily ** 2 print("方差:",variance_daily) #计算年化标准差 sigma_annualized = sigma_daily*np.sqrt(252) print("年化标准差:",sigma_annualized) #计算年化方差 variance_annualized = sigma_annualized ** 2 print("年化方差:",variance_annualized)

偏度是数据分布偏斜方向和程度的度量，反应分布的非对称性。

下图所示的曲线分别代表了负偏态和正偏态。在金融领域，人们更倾向于正的偏度，因为这意味着高盈利的概率更大。

#从scipy.stats 导入skew函数 from scipy.stats import skew #计算收益分布的偏度 returns_skewness = skew(clean_returns) print("偏好:",returns_skewness)

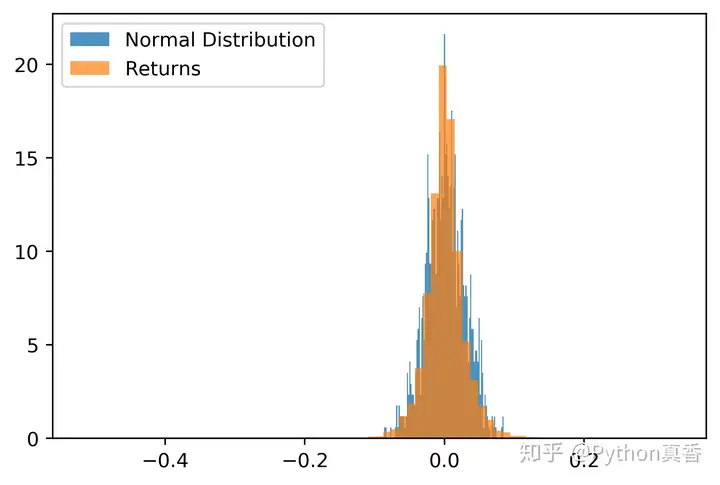
峰度表征概率密度分布曲线在平均值处峰值高低的特征数，反映了峰部的尖度。通常将样本的峰度和正态分布相比较，因为正态分布的峰度是3，所以将超出3的部分称为超值峰度。大部分金融收益都具有正的超值峰度。

上述峰度的计算结果表明，该股票收益的峰比正态分布高得多。我们也可通过下图概率密度分布的比较看出来，图中橙色代表收益的分布，而蓝色表正态分布。

#模拟正态分布数据，其均值和标准差与文中的股票收益相同。 mu = mean_return_daily sigma = sigma_daily norm = np.random.normal(mu, sigma, size=1000) #绘制正态分布概率密度分布图 plt.hist(norm,bins=100,alpha=0.8,density=True,label=Normal Distribution) #绘制收益的概率密度分布图 plt.hist(clean_returns,bins=75,alpha=0.7,density=True,label=Returns) #增加图例说明 plt.legend() #保存图片 plt.savefig("E:\stock\模拟图",dpi=400,bbox_inches=tight) #绘图 plt.show()

似乎，可以判定股票收益分布并不是正态分布，那么我们就此可以判定不是正态分布吗？我们需要使用真正的统计检验方法，而不是简单地检查峰度或偏度。只要知道如何使用p值判断数据的正态性：如果p值小于等于0.05，就拒绝正态性假设，得出数据非正态分布的结论。

#三、收益分布正态性检验 #从scipy.stats导入shapiro from scipy.stats import shapiro #对股票收益进行Shapiro-wilk检验 shapiro_results = shapiro(clean_returns) print("Shapiro-wilk检验结果:",shapiro_results) #提取p值 p_value = shapiro_results[1] print("p值:",p_value)