工程优化设计与Matlab实现——无约束问题的直接解法（三）

在无约束问题的导数解法中，我们借助梯度方向构造了“两头牛的轭”，我们称其为共轭梯度法。（详情见工程优化设计与Matlab实现——无约束问题的导数解法（四））

在这里，我们不再依赖梯度方向，而从其他角度来入手，构造共轭方向。

共轭方向法

Point 1 共轭方向与函数极值的关系

由于目标函数可以使用在任一点 x′x 二次泰勒展开式 f(x)=1/2(x−x′)T[H(x′)](x−x′)+[▽f(x′)]T(x−x′)+f(x′)f(x)=1/2(x-x)^T[H(x)](x-x)+[▽f(x)]^T(x-x)+f(x) 来近似，

从而转换为求 f(x)=1/2(x)T[H(x′)](x)+[▽f(x′)]T(x)+f(x′)f(x)=1/2(x)^T[H(x)](x)+[▽f(x)]^T(x)+f(x) 这一n元二次函数极值点的问题。

所以我们可以先以二元二次函数为例进行说明：

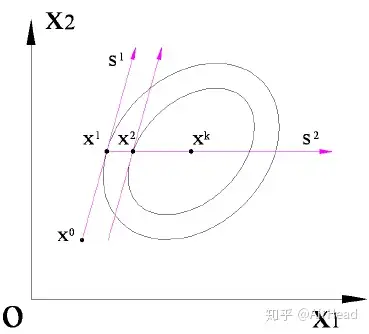
对于具有正定矩阵 GG 的二元二次函数 f(x)=1/2xTGx+bTx+cf(x)=1/2x^TGx+b^Tx+c

有两个性质：

一个是：其等值线为同心椭圆族，中心为极值点；

另一个是：过椭圆族中心的直线与椭圆交点处诸切线相互平行

根据这两个性质有如下推论：按任意搜索方向d0d_0，作同心椭圆族的两平行切线，则连接两个切点的直线通过椭圆族中心

所以，如果由 x0x_0沿 s1s_1 再沿 s2=x2−x1s_2=x_2-x_1作一维优化，即可得到极小值点xkx_k

推广到n元二次函数

对于具有 n×nn\times n 正定矩阵 AA 的n元二次函数 f(x)=1/2xTAx+BTx+cf(x)=1/2x^TAx+B^Tx+c，

其性质如下：

d1,d2,…,dnd_1,d_2,…,d_n 是关于 AA 的 nn 个非零共轭矢量，若从某一个初始点 x0x_0 出发沿任一 did_i （ i=1,2,…,ni=1,2,…,n ）方向进行一维优化搜索，得到等值线的切点，即最优点 x1x_1；再从另一初始点x0x_0 沿同一 did_i 进行一维搜索得到另一最优点 x2x_2 ，则矢量 s=x2−x1s=x_2-x_1 与矢量组 d1,d2,…,dnd_1,d_2,…,d_n 中的每一向量，关于 AA 共轭。

如果n元二次函数有n个共轭方向did_i （ i=1,2,…,ni=1,2,…,n ），从任一初始点 x0x_0 出发沿任一 did_i （ i=1,2,…,ni=1,2,…,n）方向进行一维优化搜索，可得到目标函数的极值点。

对于任意目标函数

任意目标函数 f(x)f(x) 在极值点附近都近似于一个二次函数，即：函数F(x)在极值点附近呈现较强的二次特性；一种算法如果对于二次函数的求优比较有成效，对于任意目标函数 f(x)f(x) 只要初值点选择恰当（初值点 x0x_0 离极值点 不太远），就有较好的求优效果。

Point 2 共轭方向的构成

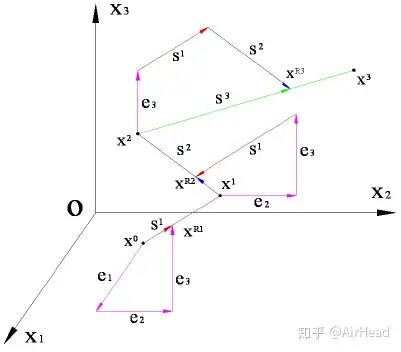
选取线性无关的坐标单位矢量 e1,e2,…,ene_1,e_2,…,e_n ，从初始点 x0x_0 出发依次沿 e1,e2,…,ene_1,e_2,…,e_n 方向作一维优化探索得 xR1x_{R1} 点，取 s1=xR1−x0s_1=x_{R1}-x_0 ，从 xR1x_{R1} 出发再沿 s1s_1 方向作一维优化探索得 x1x_1 点。

从x1x_1点出发依次沿e1,e2,…,ene_1,e_2,…,e_n，s1=xR1−x0s_1=x_{R1}-x_0方向作一维优化探索得xR2x_{R2}点，取

s2=xR2−x1s_2=x_{R2}-x_1 ，再从 xR2x_{R2} 出发沿 s2s_2 方向作一维优化探索得 x2x_2 点。

直到第n次循环，构造出 sns_n 并求得极小点 xnx_n 。

对于n元二次函数F(x)，从初始点x0x_0出发沿共轭方向s1,s2,…,sns_1,s_2,…,s_n 作n次一维优化探索，理论上 xnx_n 应为n元二次函数f(x)f(x)的极小点。

Point 3 共轭方向法的特点

共轭方向法与坐标轮换法是十分接近的，共轭方向法用构造出来的更优的共轭方向来代替原来的单位矢量方向，这就相当于对坐标轮换法的搜索方向进行了优化，使之能更快的收敛。

但是这样构造出一个方向后就将其用于计算，很可能导致迭代中的n个搜索方向有时会变成线性相关，不能形成共轭方向，导致搜索失败（如下图）。这就需要对共轭方向法进行改进——鲍威尔法（见栗子后面）。

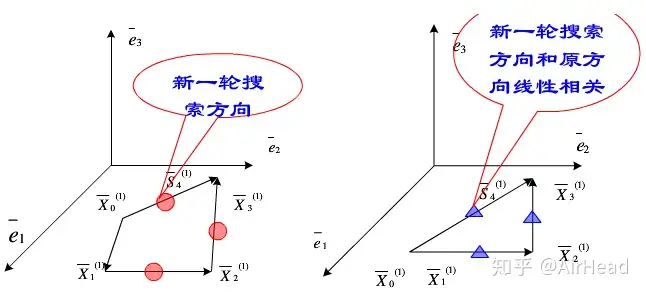
Point 4 共轭方向法的栗子

利用共轭方向法求目标函数 f(x)=10(x1+x2−5)2+(x1−x2)2f(x)=10(x_1+x_2-5)^2+(x_1-x_2)^2 ，当初始点为 [0,0]T[0,0]^T时的极小值点和极小值。

主程序：

目标函数：

共轭方向法函数：

进退法程序：工程优化设计与Matlab实现——一维搜索方法（一）

黄金分割法程序：工程优化设计与Matlab实现——一维搜索方法（二）

计算结果为：

鲍威尔法

鲍威尔法是共轭方向法的一种，克服了共轭方向法更新的搜索方向与原向量组中的向量可能出现线性相关的缺点。

具体改进如下：

在原n个方向和每轮求出的新方向（ sn+1s_{n+1} ）组成的s1,s2,s3,…,sn,sn+1s_1,s_2,s_3,…,s_n,s_{n+1} 的n+1个矢量组中有选择地去掉其中一个，成为下一轮迭代的n个方向矢量。

选择原则：所选择的n个方向矢量是线性无关的——必要条件；并最大限度地保证所选择的n个方向矢量是关于A共轭。

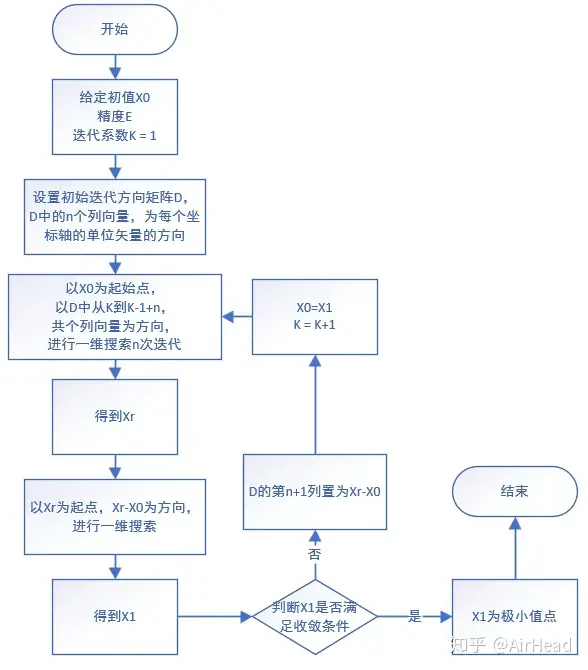
Point 1 Powell判别

初始搜索时，采用共轭方向法完成一轮迭代，即从 x0x_0 点出发依次沿任意选定的n个线性无关的初始方向 s1,s2,s3,…,sns_1,s_2,s_3,…,s_n 做一维优化后得到 x1x_1 点，并找出这一轮迭代中相邻两个迭代点函数值下降最大量，即 Δm=maxΔi=max[f(xi−1)−f(xi)]=fm−1−fm1≤i≤n\Delta_m=max\Delta_i=max[f(x_{i-1})-f(x_i)]=f_{m-1}-f_m\ \ \ \ \ \ \ 1\leq i \leq n

求出反射点 xr=x1+(x1−x0)=2x1+x0x_r=x_1+(x_1-x_0)=2x_1+x_0

若 f(xr)≥f(x0)f(x_r)\geq f(x_0) 或 [f(x0)+f(xr)−2f(x1)][f(x0)−f(x1)−Δm]2≥0.5Δm[f(x0)−f(xr)][f(x_0)+f(x_r)-2f(x_1)][f(x_0)-f(x_1)-\Delta_m]^2\geq 0.5\Delta_m[f(x_0)-f(x_r)]

则将 x1x_1 与 xrx_r 中函数值较小的那一个赋值给 x0x_0 作为下一次的初始点，下一轮迭代仍按照原方向s1,s2,s3,…,sns_1,s_2,s_3,…,s_n进行。

若 鲍威尔法流程图

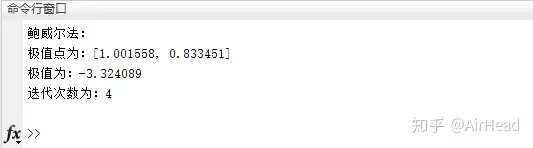
Point 2 栗子

利用鲍威尔法求目标函数 f(x)=2x13+4x1x23+x22−10x1x2f(x)=2x_1^3+4x_1x_2^3+x_2^2-10x_1x_2 在初始点为 [2,1][2,1] 时的极小值和极小值。

主程序：

目标函数定义：

鲍威尔法函数定义：

进退法程序：工程优化设计与Matlab实现——一维搜索方法（一）

黄金分割法程序：工程优化设计与Matlab实现——一维搜索方法（二）

计算结果为：