图论基础

作者：三青时间：2023-04-23 阅读数：人阅读

图的概念

图是由节点和连接节点之间的边组成的，与连线的长度，节点的位置没有关系。一个图是一个三元组<V(G), E(G), F>，其中V是一个非空的节点集合，E是边集合，F是从边集合E到节点序偶(无序偶或有序偶)集合上的函数。若图中边总是两个节点的关联，则图可简记为G=<G, E>。树可以是空树但图不能是空图。图的结点集不能为空但边集可以为空。

无向图：若图中所有边都是无向边，则图是无向图；

有向图：若所有边都是有向边，则图是有向图；

混合图：若图中既有无向边又有无向边则图为混合图；

多重图：还有平行边的任何一个图称为多重图

简单图：不含平行边和环的图称为简单图

平凡图：仅由一个孤立节点构成的图为平凡图；

零图：仅由孤立节点组成的图为零图；

完全图：图中每一对节点之间都有边相连则称为完全图

补图：给定一个图G，由图中所有节点和所有能使G称为完全图的添加边组成的图称为G相当于完全图的补图，简称G的补图。

子图：G=<V,E>，G=<V, E>，其中V,E分别是V，E的子集，则G’是G的子图

注意！图G = <V, E>是图G=<V,E>的子图，若另一子图G=<V, E>使得E=E-E，且V中仅包含E的边所关联的结点。则称 G是子图G的相对于图G的补图。

生成子图：G的子图包含G的所有结点则该子图为G的生成子图

同构图：图G=<V,E>及G=<V,E>，若存在一一对应关系g，使得v->v，e=(vi, vj) -> e = (g(vi), g(vj))，则称G于G同构记作G\simeqG.

两个图同构的充要条件是两个图的结点和边分别存在一一对应，且保持关联关系

孤立节点：图中不与任何节点邻接的节点

邻接节点：两个节点之间有边相连则这两个节点称为邻接点

邻接边：连接同一节点的两条边称为邻接边

环(回路)：邻接同一节点的一条边

度：节点连接的边数记为节点的度

出度：指出节点的边数量

入度：指向节点的边数量

定理一、节点度数总和等于边数的二倍

定理二、度数为奇数的节点必定是偶数个

定理三、所有节点入度和等于所有节点出度和

定理四、n个节点的无向完全图边数为n(n-1)/2

路

给定图G=<V, E>，设v0, v1, ...vn是图中的结点，e1, e2,...en是图中的边，ei是关联结点vi-1和vi的边，则交替序列v0e1v1e2...envn为连接v0到vn的路。

路径长度：路中边的数目记为路径长度

回路：路径初始结点和终结结点相同的路

通路：一条路中所有的结点都不相同则该路称为通路

迹：一条路中所有的边都不相同则该路称为迹

圈：回路中除了起始和终止结点相同其他都不同的路

无向图

连通：无向图中，两个结点之间存在一条路则称节点间连通

连通图：图G中只有一个连通分支

点割集：假设无向图G=<V,E>为无向图，点集V1是V的子集。若删除V1的所有结点后，所得子图不连通，但是删除V1的任何真子集后所得子图是连通图则成V1是G的一个点割集。

割点：若点割集只有一个结点，则该结点为割点

点连通度：为产生一个不连通图需要在原图(非完全图)中删除结点的最小数目

边割集：假设无向图G=<V,E>为无向图，点集E1是E的子集。若删除E1的所有边后，所得子图不连通，但是删除E1的任何真子集后所得子图是连通图则成E1是G的一个边割集。

割边：若边割集只有一个边，则该边为割边，也叫桥

边连通度：为产生一个不连通图需要在原图(非平凡图)中删除边的最小数目

有向图

可达：有向图中，结点u到结点v之间有一条路，称结点u到v可达

距离：有向图中可达的结点间最短的路径长度(无向图亦适用)

直径：图中节点对之间距离最大的长度

单侧连通：有向图中任何一对结点间至少有一个结点到另一个结点是可达的

强连通：任何一对结点之间相互可达，则图强连通

弱连通：有向图G去掉边的方向后得到的无向图是联通的则该图是弱连通

强分图：有向图中具有强连通性质的最大子图称为强分图

弱分图：有向图中具有弱连通性质的最大子图称为弱分图

单侧分图：有向图中具有单侧连通性质的最大子图称为单侧分图

定理一、在具有n个结点的图中，若vi到vj存在一条路，则vi到vj必存在一条长度不大于n-1的路

定理二、图是强连通则必是单侧连通；是单侧连通则必是弱连通。

定理三、一个有向图是强连通的，当且仅当图中有一个回路，它至少包含每个结点一次

定理四、有向图中，每个结点位于且只位于一个强分图中

图的代数表示

邻接矩阵

图的邻接矩阵表示通过使用|V|*|V|大小的方阵表示，矩阵每个元素表示结点的邻接关系。

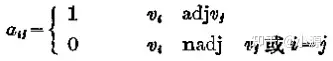
简单无向图的邻接矩阵是对称的。第i行值为1的元素数目等于结点i的出度，第j列值为1的元素数目是结点j的入度。

定理一、A为图的邻接矩阵，A^n中第i行第j列的元素等于结点i和结点j之间长度为n的路的数目

可达矩阵

对于一个简单有向图G，假设图中节点已排序，则方阵P为图G的可达矩阵

可达矩阵表明图中任意两个结点之间是否存在一条路。可达矩阵的计算通过邻接矩阵A计算。

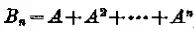
将B中不为零的元素替换为1，得到的矩阵就是可达矩阵。

完全关联矩阵

给定图G，v1,v2,...vn和e1,e2,...eq分别为G中的点和边，则M为图的完全关联矩阵

无向图

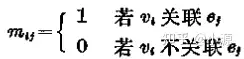
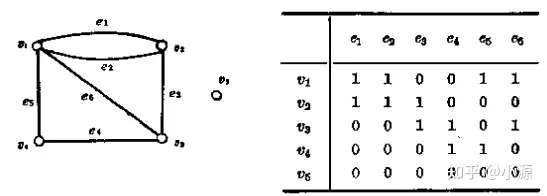
有向图

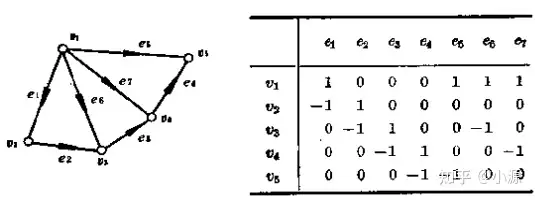
完全关联矩阵中两行相加(相当于两个结点合并)

1）有向图中是两行分量的普通加法运算

2）无向图中是对应分量加法模2运算

拉普拉斯矩阵

对于具有n个节点的简单无向图，该图拉普拉斯矩阵L定义为

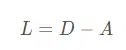
D为图的度矩阵，是一个n*n的对角矩阵，diag(v)是v的度

对称归一化拉普拉斯矩阵

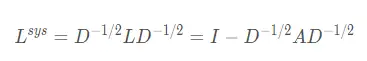
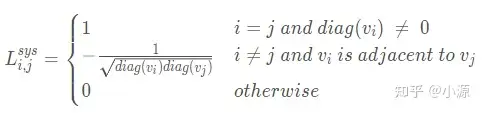
随机游走归一化拉普拉斯矩阵

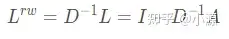
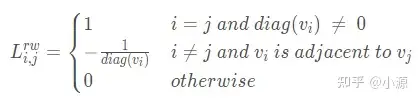
定理：

a. 拉普拉斯矩阵半正定

b. 拉普拉斯矩阵特征值非负

c. 最小非零特征值是图的代数连通度

d.特征值为0的数目是连通分量数目

e.对称归一化的拉普拉斯矩阵的特征值[0,2]

欧拉图与汉密尔顿图

欧拉路径：无孤立结点图中，每个边恰好只被访问一次(有向图中欧拉路叫单向欧拉路)

欧拉回路：一条回路，图中每条边访问且只访问一次

欧拉图：具有欧拉回路的图称作欧拉图

哈密尔顿路径：每个结点恰好只被访问一次

哈密尔顿回路：一条回路，每个结点恰好只被访问一次

哈密尔顿图：具有哈密尔顿回路的图称作哈密尔顿图

闭包：图G有n个结点，若将图G中度数之和至少是n的非邻接结点连接起来得图G，对图G重复上述步骤，直到不再有这样得结点对存在为止后得到得图称为原图G的闭包

定理一、无向图G具有一条欧拉路，当且仅当G是连通的，且有零个或两个奇数度结点

推论一、无向图G具有一条欧拉回路，当且仅当G是连通的，且所有结点度数全为偶数

定理二、图G有汉密尔顿回路，则结点集V的每个非空子集S均有G-S的连通分支数小于等于|S|

定理三、图G具有n个结点的简单图，若图中每一对结点度数之和大于等于n-1，则在G中存在一条汉密尔顿路

定理四、图G具有n个结点的简单图，若图中每一对结点度数之和大于等于n，则在G中存在一条汉密尔顿回路

定理五、当且仅当一个简单图的闭包是汉密尔顿图时，该简单图是汉密尔顿图

平面图

平面图：图G是一个无向图，若把G的所有结点和边画在平面上，且使得任何两条边除了端点外没有其它交点，称该图是一个平面图

面：G是一连通平面图，图中边包围的区域内没有结点和边，该区域叫G的一个面

边界：包围面的边构成的回路叫该面的边界

2度结点内同构：若两个图同构或者通过反复插入或删除度为2的结点后同构，则称两个图在2度结点内同构

定理一、一个有限平面图，面的次数之和等于其边数的两倍

定理二、欧拉定理，一个连通的平面图，v个结点e条边和r个面，欧拉公式：v-e+r=2

定理三、G是一个有v个结点e条边的连通简单平面图，若v>=3,则e<=3v-6

对偶与着色

对偶图：给定平面图G=<V, E>，它具有面F1, F2,...Fn，若图G*=<V*, E*>满足一下条件则陈G*是G的对偶图。

a. 图G任意一个面Fi，内部有且仅有一个结点v*i属于V*

b. 图G的面Fi, Fj公共边界ek，存在且仅存在一条边e*k，使e*k=(v*i, v*j)，且e*k与ek相交

c. 当且仅当ek只是一个面Fi的边界时，v*i存在一个环e*k和ek相交。

自对偶图：图G的对偶图同构于G，则G是自对偶图

着色：给定一平面图，对每个结点着色使相邻结点颜色不同。着色用了n种颜色则图称为n色的。

韦尔奇。鲍威尔法对图着色：

a. 将图G种结点按照度数递增次序进行排列

b. 用第一种颜色对第一点着色，并按照排列次序，对前面着色不相邻的结点着相同颜色

c. 用第二种颜色对未着色点重复b操作，第三种颜色继续此法，直到所有结点都着上

定理一、对于n个结点的完全图Kn，着色数为n

定理二、一个至少具有三个结点的连通平面图，则G中必有一个结点u使得deg(u)<=5

定理三、任意平面图最多是5色的

数与生成树

树：连通无回路的无向图

森林：无回路的无向图，其每个连通分图是树

树叶：树种度为1的结点

分支点：树中度数大于1的结点

生成树：图的生成子图是棵树，则该树是图的生成树

最小生成树：图中所有生成树中树权(所有边权和)最小的生成树

弦：图G中不在生成树中的边称作弦

补：弦的集合

最小生成树算法：

a) Kruskal算法(边)

对图中边按照权值升序排序选取权值最小的边，判断加入该边后生成的树是否产生回路，若没有就加入，若有则舍弃重复步骤2，直到所有点都加入

b)Prim算法(点)

定义一个顶点集合S和边集合E，初始都为空选取任意顶点X加入S选取权值最小的边(X,Y)，X在S中Y不在S中，将Y并如S，边并入E重复步骤３直到所有点都加入S

定理一、任一棵树至少有两片树叶

定理二、连通图至少有一棵生成树

定理三、一条回路和任何一棵生成树的补至少有一条公共边

定理四、一个边割集和任何生成树至少有一条公共边

根树

有向树：当有向图不考虑边方向时是一棵树，该有向图称为有向树

根树：有向树种只有一个结点入度为0，其余结点入度为1。其中入度为0的结点叫根，出度为0的结点叫叶

m叉树：根树中每个结点出度小于等于m

完全m叉树：根树中每个结点出度恰好等于m或0

正则m叉树：所有树叶层次相同

通路长度：从树根到该结点的通路中的边数。分支点的通路长度称为内部通路长度，树叶的通路长度称为外部通路长度

最优树：同最小生成树

定理一、有完全m叉树，树叶数为t，分支点数为i，则(m-1)i = t-1

定理二、完全二叉树有n个分支点，且内部通路长度总和为I，外部通路长度总和为E则E=I+2n

图的存储

邻接矩阵

图的邻接矩阵通过使用|V|*|V|大小的方阵表示，矩阵每个元素表示结点的邻接关系。

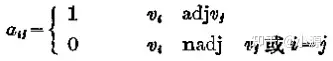
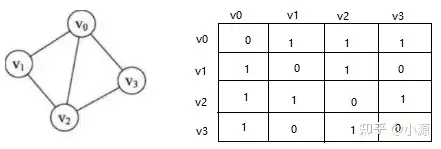
简单无向图的邻接矩阵是对称的。第i行值为1的元素数目等于结点i的出度，第j列值为1的元素数目是结点j的入度。对于带权图，则矩阵的元素表示边的权重。

邻接表

图的邻接矩阵的空间复杂度巨大，通常是稀疏的。对于无向图可以采用压缩矩阵的方式存储但是对于有向图会存在大量空间浪费，因此人们设计了邻接表的方式存储。

邻接表方式主要由顺序存储和链表存储两种方式构成。图中所有结点采用顺序存储方式，对于每个结点对应一条边表(单链表)，表示该结点邻接的所有结点，对于有向图而言，边表则是有向边指向的所有结点。

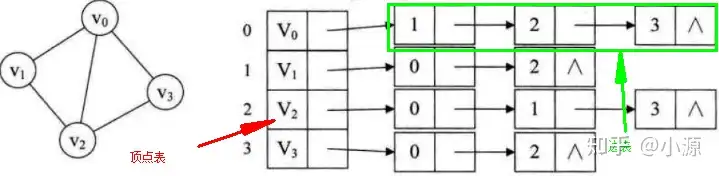
邻接表中有两个基本数据结构，顶点表结点和边表结点。顶点表结点主要存放节点的属性信息和指向第一个表边结点的指针信息。边表结点存放着边另一头结点的Id等信息(代表一条边)和指向下一个边表结点的指针。值得注意的是，同一个图，对应邻接表不一定唯一。因为根据构造顺序的不同，结果不同。

十字链表

邻接表表示有向图时，每个结点对应的边表表示结点的出度信息，无法表示入度信息。可以采用逆邻接矩阵的方式表示出度信息但不能表示入度信息，因此，考虑将邻接表与逆邻接表结合同时表示有向图的出入度信息，得到十字链表的表示方式。

十字链表是邻接表的加强版，是在邻接表的基础上同时考虑出入度信息。十字链表同样包含两个数据结构即顶点表结点和边表结点。顶点表结点包含三个部分分别是结点的属性信息，出度域和入度域。出度域指向该结点的所有出边构成的边表，入度域指向以该结点为终点的所有边结点构成的边表。边结点上包含着该有向边的头尾所连的结点和同头同尾的指针域，这样，弧头相同的会连在同一链表上，弧尾相同的会连在同一链表上。十字链表中有多少结点，结点表就有多少项，有多少边，边表就有多少项。