【升级の高中数学／导数】函数逼近的三种方法——泰勒展开、帕德逼近与洛朗级数

 

upd 2022.6.25：修改了部分typo

好久不见！

前言

当我们在研究解决高中数学中函数／导数相关的问题时，经常需要用到一些不等式或函数逼近的结论，这些结论用多项式或分式进行拟合，将既定的超越函数转化为易操作的代数函数，从而便于不等式的证明或对特定函数值的估计．例如不等式ex⩾x+1e^x\geqslant x+1 这一函数逼近结论已经在各大模拟题中用烂了．而一些更精确的逼近与放缩，如 ln⁡(x+1)⩽6x+x24x+6\ln(x+1)\leqslant \dfrac{6x+x^2}{4x+6}，也有时在较难的题目中成为证出关键结论的救命稻草．

因此，一个很自然的想法是：对函数的逼近程度越高，拟合得越接近，放缩的效果越好，解决给定题目的能力可能就越大．

于是我们会问：怎么去找到一个函数的较好逼近呢？

本文在这里介绍三种函数逼近的方法——泰勒展开（Taylor Expansion） 、 帕德逼近（Padé Approximant） 和洛朗级数（Laurent Series），其中第一种大家都很熟悉了，是常见的多项式逼近；后面两者为分式逼近，在对函数的逼近中一般更为精确．

以下，我们进入正文．

如有错误，欢迎各位指正．

一、泰勒展开（Taylor Expansion）

1.1 从切线拟合讲起

相信大家都见过以下的几个常用不等式：

ex⩾x+1,ln⁡x⩽x−1,ex⩾ex⋯e^x\geqslant x+1,\quad \ln x\leqslant x-1,\quad e^x\geqslant ex\cdots

这几个不等式可谓是家喻户晓了，其中第一个不等式 ex⩾x+1e^x\geqslant x+1更可以说是许多人在接触超越函数放缩时见到的第一个不等式．后面两个不等式可以说是第一个不等式的变形，也是很常用的不等式．

而具体而言，这样的不等式背后有一个共同的特征： 将具凹凸性的超越函数用其某点处的切线拟合． 例如由函数f(x)=exf(x)=e^x 的凸性及点 (0,f(0)),(1,f(1))(0,f(0)),\ (1,f(1)) 处的切线，可得第一、第三个不等式；由函数 f(x)=ln⁡xf(x)=\ln x 的凹性及点(1,f(1))(1,f(1)) 处的切线，可以得到第二个不等式等．像这样的拟合方法，我个人称为切线拟合．

切线拟合的一大优势在于对切点附近的拟合程度相当好．这不仅是因为切点在原来的函数上，更是因为它拟合了函数在切点处的变化趋势，即拟合了函数在切点处的导数值．正是这一点，切线拟合及切线放缩在高中范围研究函数中有较广泛的应用

当然，结合图象可以看出，这种拟合方式还是很粗线条的．为此，我们想要找到一个更精确的拟合方法．而切线拟合的拟合方法给了我们启示：既然用一阶导数逼近就可以在切点附近达到一定的精度，那多导几次，让拟合函数在某点处的任意阶导数与原函数的同阶导数相等，精度也许会更高．

而这正是泰勒展开的思想：构造一个多项式（因为多项式好求导），调一调系数，让它在某点处的任意阶导数与原函数的同阶导数相等．

1.2 麦克劳林级数（Maclaurin Series）与泰勒级数（Taylor Series）

对给定的函数 f(x)f(x) 及其定义域内一点 x0x_0，为用一个 nn 次多项式去拟合该函数，考虑一个nn次多项式 p(x)=a0+a1x+a2x2+a3x3+⋯+anxnp(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots+a_nx^n，满足:

p(x0)=f(x0)p′(x0)=f′(x0)p″(x0)=f″(x0)p(3)(x0)=f(3)(x0)⋯p(n)(x0)=f(n)(x0)\begin{aligned}p(x_0)&=f(x_0)\\p(x_0)&=f(x_0)\\p(x_0)&=f(x_0)\\p^{(3)}(x_0)&=f^{(3)}(x_0)\\&\cdots\\p^{(n)}(x_0)&=f^{(n)}(x_0)\end{aligned}

则我们可以认为：满足该条件的多项式在 x0x_0 处对函数 f(x)f(x) 有较好的拟合效果．

下面我们来讨论如何去求这样的多项式．

首先，考虑到 p(x0)p(x_0) 形式不太方便，我们变形成

p(x)=b0+b1(x−x0)+b2(x−x0)2+⋯+bn(x−x0)np(x)=b_0+b_1(x-x_0)+b_2(x-x_0)^2+\cdots+b_n(x-x_0)^n

其中 {bn}\{b_n\} 是常数列．这样则得

p(x0)=b0p′(x0)=b1p″(x0)=2b2⋯p(n)(x0)=n!bn.\begin{aligned}p(x_0)&=b_0\\p(x_0)&=b_1\\p(x_0)&=2b_2\\&\cdots\\p^{(n)}(x_0)&=n!b_n.\end{aligned}

因此比对系数有

bk=f(k)(x0)k!(k=0,1,2,⋯,n)b_k=\dfrac{f^{(k)}(x_0)}{k!}\quad (k=0,1,2,\cdots,n)

这样就给出了 f(x)f(x) 在点 (x0,f(x0))(x_0,f(x_0)) 处的 nn 次多项式逼近，即

pn(x)=f(x0)0!+f′(x0)1!(x−x0)+f″(x0)2!(x−x0)2+⋯+f(n)(x)n!(x−x0)n.p_n(x)=\dfrac{f(x_0)}{0!}+\dfrac{f(x_0)}{1!}(x-x_0)+\dfrac{f(x_0)}{2!}(x-x_0)^2+\cdots+\dfrac{f^{(n)}(x)}{n!}(x-x_0)^n.

注意到无论 nn 取多少，前 nn 项的取值都与 nn 无关，因此我们大胆一点：直接令 n→∞n\to \infty！这样我们就得到无穷项多项式

p(x)=f(x0)0!+f′(x0)1!(x−x0)+f″(x0)2!(x−x0)2+⋯+f(n)(x)n!(x−x0)n+⋯p(x)=\dfrac{f(x_0)}{0!}+\dfrac{f(x_0)}{1!}(x-x_0)+\dfrac{f(x_0)}{2!}(x-x_0)^2+\cdots+\dfrac{f^{(n)}(x)}{n!}(x-x_0)^n+\cdots

该式称为函数 f(x)f(x) 在点 (x0,f(x0))(x_0, f(x_0))处的泰勒级数．特别地，当x0=0x_0=0 时，该式又称为函数 f(x)f(x) 的麦克劳林级数．以下我们统称为泰勒级数．

求出一个函数在某点处泰勒级数的方法称为泰勒展开．下面，我们来求解一些高中范围内常用的泰勒级数．

1.3 高中范围内常见的泰勒级数

首先看指数函数 f(x)=exf(x)=e^x ，其任意阶导数 f(n)(x)=exf^{(n)}(x)=e^x．令x0=0x_0=0，由上面的公式可得

ex=1+x+x22!+x33!+⋯=∑i=k∞xkk!.(1.1)\color{black}\displaystyle e^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots=\sum_{i=k}^\infty \dfrac{x^k}{k!}.\quad (1.1)

再看简单的三角函数 sin⁡x\sin x 和 cos⁡x\cos x．取x0=0x_0=0，同样容易得到

sin⁡x=x−x36+x5120+⋯=∑k=0∞(−1)k(2k+1)!x2k+1.(1.2)\color{black}\displaystyle\sin x=x-\dfrac{x^3}{6}+\dfrac{x^5}{120}+\cdots=\sum_{k=0}^\infty \dfrac{(-1)^k}{(2k+1)!}x^{2k+1}.\quad (1.2)

cos⁡x=1−x22+x424+⋯=∑k=0∞(−1)k(2k)!x2k.(1.3)\color{black}\displaystyle\cos x=1-\dfrac{x^2}{2}+\dfrac{x^4}{24}+\cdots=\sum_{k=0}^\infty \dfrac{(-1)^k}{(2k)!}x^{2k}.\quad (1.3)

下面考虑对数函数 f(x)=ln⁡(x+1)f(x)=\ln (x+1) 的泰勒级数（这里因为 y=ln⁡xy=\ln x 的定义域 (0,+∞)(0,+\infty)，我们做一下平移）．为此，我们先考虑以下的展开：

11−x=1+x+x2+⋯=∑k=0∞xk.(1.4)\color{black}\displaystyle\dfrac{1}{1-x}=1+x+x^2+\cdots=\sum_{k=0}^\infty x^k.\quad (1.4)

即函数 g(x)=11−xg(x)=\dfrac{1}{1-x}对x0=0x_0=0 的展开．因此我们有

f′(x)=11+x=1−x+x2−x3+⋯=∑k=0∞(−1)kxk.f(x)=\dfrac{1}{1+x}=1-x+x^2-x^3+\cdots=\sum_{k=0}^\infty(-1)^kx^k.

两边同时积分并待定常数、取 x=0x=0 可得

ln⁡(x+1)=x−x22+x33+⋯=∑k=1∞(−1)k−1kxk.(1.5)\displaystyle\ln (x+1)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}+\cdots=\sum_{k=1}^\infty \dfrac{(-1)^{k-1}}{k}x^k.\quad (1.5)

对较复杂的三角函数f(x)=tan⁡xf(x)=\tan x，其泰勒展开式十分复杂，超出了高中的处理范围，在此我们只给出结论，不讨论它的具体求解了．

tanx=x+x33+215x5+17315x7+⋯=∑k=1∞(22k−1)22kBk(2k)!x2k−1.(1.6)\displaystyle \color{black}\tan x=x+\dfrac{x^3}{3}+\dfrac{2}{15}x^5+\dfrac{17}{315}x^7+\cdots=\sum_{k=1}^\infty \dfrac{(2^{2k}-1)2^{2k}B_k}{(2k)!}x^{2k-1}.\quad (1.6)

这里BkB_k 为第 kk 个伯努利数的偶数项的绝对值．

1.4 泰勒展开的应用——所谓的「泰勒放缩」

泰勒展开这一逼近方法当然有许多应用，但鉴于研究领域为高中数学，我们主要研究其中的一种重要应用：即所谓泰勒放缩．泰勒放缩的方法很简单粗暴：直接将展开式中后面的高次项丢掉即可．

一个简单的例子：对 y=ex=1+x+12x2+⋯y=e^x=1+x+\dfrac{1}{2}x^2+\cdots，我们在二次项处截断，即得ex⩾1+x+12x2e^x\geqslant 1+x+\dfrac{1}{2}x^2 对任意 x⩾0x\geqslant 0 成立．值得注意的是，如果在一次项处截断，可以看到正好符合切线放缩的形式．

二、帕德逼近（Padé Approximant）

2.1 帕德逼近的介绍

泰勒展开是一种很好的逼近方法，对许多函数都有着很好的效果．然而，有时泰勒展开对某些带极值的函数逼近的效果却不尽人意，本质原因是多项式级数的局限性．为此，我们转而考虑用分式来逼近函数，即所谓分式逼近．一种分式逼近的最常用方法称为帕德逼近．

帕德逼近的思想与泰勒展开是类似的．其想法如下：对某个函数 f(x)f(x)，考虑一个分式rm/n(x)=pm(x)qn(x)r_{m/n}(x)=\dfrac{p_m(x)}{q_n(x)}，这里 pm(x)p_m(x)、qn(x)q_n(x) 分别为 mm、nn次多项式．我们想找到这样的分式，使得对一点x0x_0 有：

f(x0)=rm/n(x0)f′(x0)=rm/n′(x0)f″(x0)=rm/n″(x0)⋯f(m+n)(x0)=rm/n(m+n)(x0)\begin{aligned}f(x_0)&=r_{m/n}(x_0)\\f(x_0)&=r_{m/n}(x_0)\\f(x_0)&=r_{m/n}(x_0)\\&\cdots\\f^{(m+n)}(x_0)&=r^{(m+n)}_{m/n}(x_0)\end{aligned}

如果这样的分式 rm/n(x)r_{m/n}(x) 存在，我们就称其为原函数的一个帕德逼近．

2.2 帕德逼近的求解

下面我们来求解一个函数在 x0x_0 处的帕德逼近．

首先，对函数f(x)f(x)，我们先考虑它在 x0x_0 处的泰勒展开（当然如果该函数是多项式，其泰勒展开就是本身）．设

f(x)=a0+a1x+a2x2+⋯=∑k=0∞akxkf(x)=a_0+a_1x+a_2x^2+\cdots=\sum_{k=0}^\infty a_kx^k

我们只需考虑如下的方程

f(x)−pm(x)qn(x)=0f(x)-\dfrac{p_{m}(x)}{q_n(x)}=0

由系数的齐次性，不妨设qn(0)=1q_n(0)=1．令 pm(x)=p0+p1x+p2x2+⋯+pmxmp_m(x)=p_0+p_1x+p_2x^2+\cdots+p_mx^m，qn(x)=q0+q1x+q2x2+⋯+qnxnq_n(x)=q_0+q_1x+q_2x^2+\cdots+q_nx^n，代入、乘开得方程组

{a0=p0a1+a0q1=p1a2+a1q1+a0q2=p2⋯am+am−1q1+am−2q2+⋯+a0qm=pmam+1+amq1+am−1q2+⋯+am−n+1qn=0⋯am+n+am+n−1q1+am+n−2q2+⋯+amqn=0\begin{cases}a_0&=p_0\\a_1+a_0q_1&=p_1\\a_2+a_1q_1+a_0q_2&=p_2\\\cdots\\a_m+a_{m-1}q_1+a_{m-2}q_2+\cdots+a_0q_m&=p_m\\a_{m+1}+a_mq_1+a_{m-1}q_2+\cdots+a_{m-n+1}q_n&=0\\\cdots\\a_{m+n}+a_{m+n-1}q_1+a_{m+n-2}q_2+\cdots+a_{m}q_n&=0\end{cases}

这里设当 k>nk>n 时，qk=0q_k=0．解得

rm/n(x)=|am−n+1am−n+2⋯am+1⋮⋮⋱⋮amam+1⋯am+n∑j=nmaj−nxj∑j=n−1maj−n+1xj⋯∑j=0majxj||am−n+1am−n+2⋯am+1⋮⋮⋱⋮amam+1⋯am+nxnxn−1⋯1|.\color{red}{\color{black}\displaystyle r_{m/n}(x)=\dfrac{\left|\begin{matrix}a_{m-n+1} &a_{m-n+2} &\cdots &a_{m+1}\\\vdots&\vdots &\ddots&\vdots\\a_m&a_{m+1}&\cdots&a_{m+n}\\\displaystyle \sum_{j=n}^ma_{j-n}x^j&\displaystyle \sum_{j=n-1}^ma_{j-n+1}x^j&\cdots&\displaystyle \sum_{j=0}^ma_{j}x^j \end{matrix}\right|}{\left|\begin{matrix}a_{m-n+1}&a_{m-n+2}&\cdots&a_{m+1}\\\vdots&\vdots&\ddots&\vdots\\a_{m}&a_{m+1}&\cdots&a_{m+n}\\x^n&x^{n-1}&\cdots&1\end{matrix}\right|}}.

此即函数 f(x)f(x) 在 x0x_0 处的 m/nm/n 型帕德逼近．

当然，手算这坨鬼玩意儿是会死人的，我们照样给出具体的例子．

2.3 常用的帕德逼近式

帕德逼近常用于指数与对数函数．下面是一些常用的帕德逼近式．（参考了@零号的鬼的本篇文献）

e^x

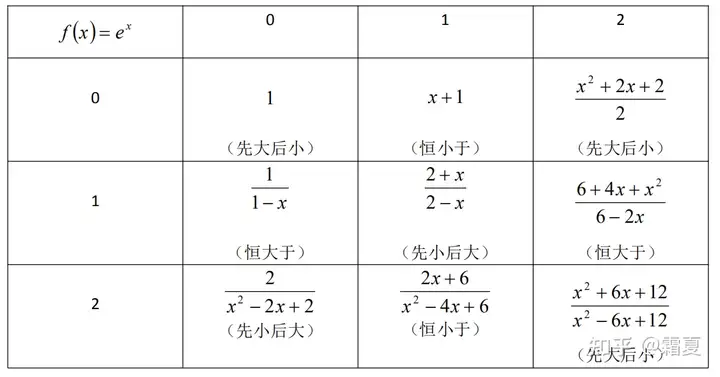
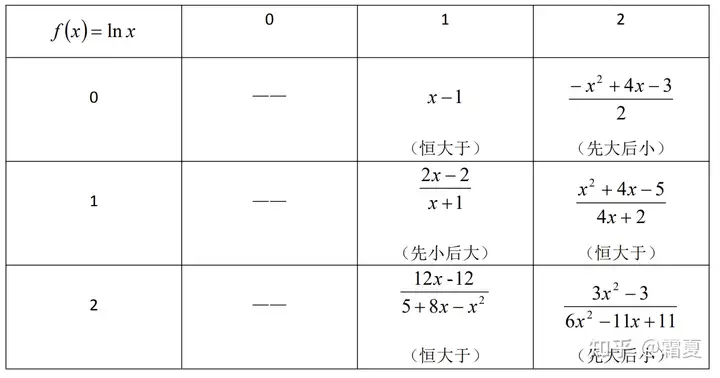
此外，对函数 f(x)=ln⁡xf(x)=\ln x，一个较为常用的估计式是x2−12x\dfrac{x^2-1}{2x}，该分式对函数也有较好的拟合效果．

三、洛朗级数（Laurent Series）方法

3.1 洛朗级数的介绍

帕德逼近的逼近程度极高，然而帕德逼近也有其问题．一方面，其计算量过大（可以看出那个行列式不是人算的），只适合电脑证明．另一方面，有时帕德逼近的结果不能使人满意（对于无极值点的函数，甚至有时不如泰勒展开）．因此，本文再介绍一种逼近方法：洛朗级数．

洛朗级数是对复变函数的一种逼近方法，它同时用分式与多项式进行逼近．其逼近式类似于如下形式：

f(z)=∑k=−∞∞ak(z−c)k=P(1z−c)+Q(z−c)f(z)=\sum_{k=-\infty}^\infty a_k(z-c)^k=P\left(\dfrac{1}{z-c}\right)+Q(z-c)

这里 P(x)P(x)、Q(x)Q(x) 是多项式．其中P(1z−c)P\left(\dfrac{1}{z-c}\right)称为主部，Q(z−c)Q(z-c)

称为正则部．

需要注意的是：由洛朗级数的性质，我们并非对原函数进行洛朗级数展开．反之，我们是通过构造一个满足条件的函数，然后用泰勒级数及代数变形解决问题．因此，与其说后文是对洛朗级数的计算，不如说是洛朗级数方法的运用．

3.2 洛朗级数方法的运用

对一个给定的函数 f(x)f(x)，考虑其在 x0x_0 处的泰勒展开

f(x)=a0+a1(x−x0)+a2(x−x0)2+⋯=∑k=0∞ak(x−x0)kf(x)=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\cdots=\sum_{k=0}^\infty a_k(x-x_0)^k

构造一个函数 g(x)=1f(x)−a0−a1(x−x0)−⋯−an(x−x0)ng(x)=\dfrac{1}{f(x)-a_0-a_1(x-x_0)-\cdots-a_n(x-x_0)^n}，则 x→x0x\to x_0 时，有g(x)→∞g(x)\to \infty．我们只需找出 g(x)g(x) 在洛朗级数下的主部即可．

洛朗级数的计算式是

f(z)=12πi∑k=−∞∞(z−c)k∮Ωf(z)(z−c)k+1dzf(z)=\dfrac{1}{2\pi i}\sum_{k=-\infty}^{\infty}(z-c)^k\oint_{\Omega}\dfrac{f(z)}{(z-c)^{k+1}}\mathrm dz

这当然不是我们高中生能做的．因此，我们考虑用另外的方法计算．

用泰勒展开的前 mm 项（n">m>nm>n）替换 f(x)f(x)，得到

g(x)∼1an+1(x−x0)n+1+an+2(x−x0)n+2+⋯+am(x−x0)m=1an+1(x−x0)n+1⋅11+an+2an+1(x−x0)+an+3an+1(x−x0)2+⋯+aman+1(x−x0)m−n−1\begin{aligned}g(x)&\sim\dfrac{1}{a_{n+1}(x-x_0)^{n+1}+a_{n+2}(x-x_0)^{n+2}+\cdots+a_m(x-x_0)^m}\\&=\dfrac{1}{a_{n+1}(x-x_0)^{n+1}}\cdot \dfrac{1}{1+\frac{a_{n+2}}{a_{n+1}}(x-x_0)+\frac{a_{n+3}}{a_{n+1}}(x-x_0)^2+\cdots+\frac{a_m}{a_{n+1}}(x-x_0)^{m-n-1}}\end{aligned}

对右侧函数运用式(1.4)(1.4)（还记得吗）的前若干项来展开，即可得一个负次数+正次数的幂级数．

下面我们进行判阶．判阶的依据是我们所得到某一阶的洛朗级数的下一阶是否展开完毕，方法是用更高阶的泰勒级数替换，然后等比展开看系数．具体而言，若上述展开的级数中，其最高次项恰为常数项（零次项），则说明用于替换的泰勒级数足够展开到洛朗级数的最低次幂，该式就是较好的展开式主部．否则就需在上述步骤中用m+1m+1 替换 mm，看看常数项有没有变化．若没有变化就说明判阶成功；若有变化，则还需继续向上增加mm，直到找到一个合适的 mm．

最后，判阶成功后，就可以用 g(x)g(x) 的展开式反解出原来的函数 f(x)f(x) 的展开式了．

3.3 洛朗级数展开得到的相关结论

以下是借助洛朗展开可得到的一些结论．