数值分析-函数逼近&&插值、函数逼近&曲线拟合的区别

 

一、注意插值、函数逼近、曲线拟合的区别：

插值：没有原函数概念，是给定一些点，要求出一个简单函数，使得该简单函数通过所有点，或者更进一步，要求简单函数的一阶、二阶导数等于某些值或者分段插值时在分段点的左右一阶、二阶导数相等，或者还有其他条件等等。

函数逼近：已知原函数的情况下，找一个简单函数逼近于原函数，使得在定义域上的某个点的误差达到最小（这个点是误差达到最大值的点）。

曲线拟合：原函数未知，给定原函数的若干点，在某个简单函数空间找出使得总误差（根据不同定义有不同的误差距离的衡量，一般是均方误差）最小的那个简单函数。而且这个函数要根据特定的问题设计特定的形式。

二、函数逼近

这里主要讲多项式的逼近方法。

1、正交多项式

其中权函数定义：

正交多项式的定义：

其中 {φ(xn)}0∞\left\{ \varphi(x_{n}) \right\}_{0}^{\infty}表示所有线性无关的多项式生成的无限维线性空间。

正交多项式的性质：

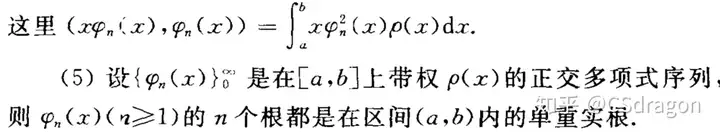
2、勒让德正交多项式

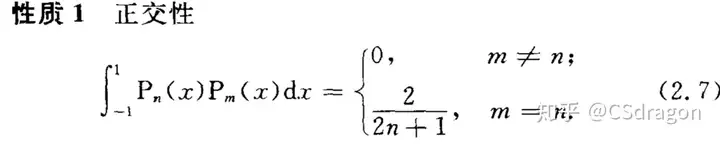
性质2 ：奇偶性

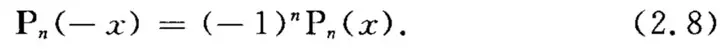
性质3：递推关系

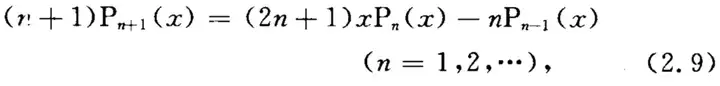
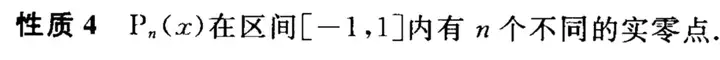
2、切比雪夫正交多项式

根据选取的权函数不同，由 {x,x2,...,xn,...}\left\{ x, x_{2}, ..., x_{n}, ... \right\} 正交化得到不同的正交化多项式。

3、最佳一致逼近多项式

误差定义：

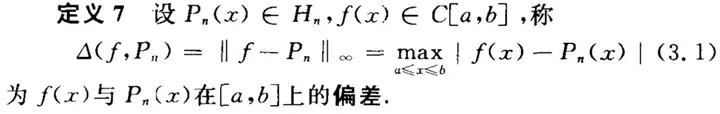
最佳一致逼近多项式定义：可以证明最佳一致逼近多项式是一定存在的。在最佳一致逼近多项式中误差达到最大的点叫做偏差点。

最佳一致逼近多项式的充要条件：

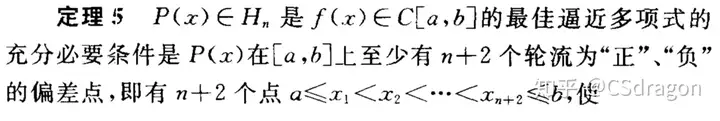
一般情况下用定理五计算P(x)比较难，应用定理六解决一些简单问题：

4、最佳平方逼近

定义：

推导过程：(4.1)问题等价于求 I(a0,a1,...,an)I\left( a_{0}, a_{1}, ..., a_{n} \right) 的最小值。

举个例子：