数值分析(7)：函数逼近

作者：三青时间：2023-05-29 阅读数：人阅读

更多数值分析内容，欢迎关注笔者@ReEchooo

同时也可以关注以下数值分析专栏：

数值分析点点滴滴www.zhihu.com/column/c_1358712114258018304

1. 引言

在前面章节《数值分析(6)：分段低次插值和三次样条插值》和《数值分析(5)：插值法》中已经介绍了如何用给定的插值点进行插值，得到的插值函数能够精确地经过这些给定的插值点。但是如果这些点本身就不精确，那么我们就没必要精确地经过这些点，只要保证在插值函数多项式的次数较低的情况下，和这些点保持一个较小的误差即可，即函数逼近。

首先来看代数多项式空间的概念：

再来看函数空间的概念：

显然函数空间是由函数组成的，满足加法和数乘运算的线性空间。

对于函数逼近，有以下的魏尔斯特拉斯定理

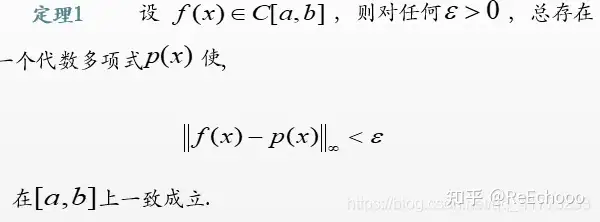
伯恩斯坦1912年给出的证明是一种构造性证明.他根据函数整体逼近的特性构造出伯恩斯坦多项式，即：

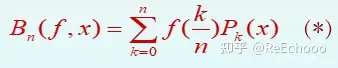
其中：

这个结果不但证明了定理1，而且由(*)给出了的一个逼近多项式，但它收敛太慢，实际中很少使用。

更一般的情况是，用函数空间的子空间 Φ\Phi 来求解一个函数 φ∗(x)\varphi^*(x) 来逼近原函数 f(x)f(x)，即：

本章的逼近问题即为：在某个函数空间 Φ\Phi 中求出 φ(x)\varphi(x) ,使得：

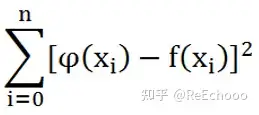
最小，即曲线拟合的最小二乘法。

2. 预备知识

1.多元函数极值的必要条件：偏导数等于0.(非充分条件)

2.向量内积的定义与其四条性质：

关于内积空间中的是否向量线性无关（注意线性无关并不一定正交），可以用以下的gram矩阵判断，即：

3.权函数的定义与带权内积的定义权函数的定义如下：

带权内积的定义如下：

可以证明，带权内积也满足内积的四条性质，那么根据带权内积可以定义连续加权⒉范数，即：

4.向量的加权内积

向量的加权内积定义如下

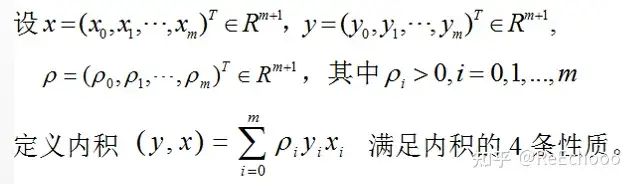
5.离散权函数的带权内积

离散权函数的带权内积定义如下：

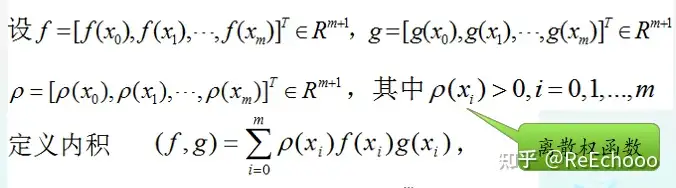
离散加权2范数:

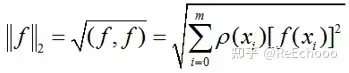
6.函数组的线性相关，线性无关

对于 ii 次多项式，有以下命题：

3. 正交多项式

3.1 正交多项式的定义和性质

根据前述的带权内积的定义，可以定义带权的正交多项式，也就是带权内积为0的多项式序列中的多项式。

如果一个多项式满足以下定义：

那么称该多项式序列 {φn(x),n≥0}\{ \varphi_n(x),n \geq0 \} 是在 [a,b][a, b] 上带权函数 ρ(x)\rho(x)正交，并称φn(x)\varphi_n(x) 为 [a,b][a, b] 上带权函数 ρ(x)\rho(x) 的 nn 次正交多项式。

如果给定了区间 [a,b][a, b] 和权函数 ρ(x)\rho(x)，那么构造正交多项式可以用以下方法：

其中：

Cj=(xn,φj(x))(φj(x),φj(x))C_j=\frac{(x^n,\varphi_j(x))}{(\varphi_j(x),\varphi_j(x))}

正交多项式的性质有以下六条：

注意第六个性质是非常强的，n次多项式必有n个根，但是未必是不同的，实的，并且都被限制在某个区间内的。

3.2 几个常用的正交多项式

Legendre多项式

定义：

性质：

2.Chebyshev多项式

定义：

性质：

3.Laguerre多项式

定义：

性质：

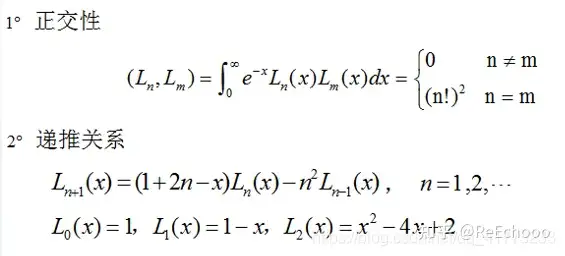
4.Hermite多项式

定义：

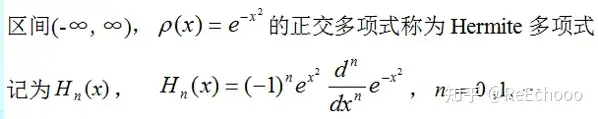
4. 最佳平方逼近

在介绍最佳平方逼近之前，首先来看函数二范数的定义：

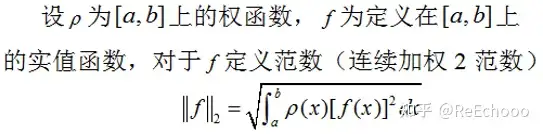
如果函数二范数是有界的，那么有如下记号：

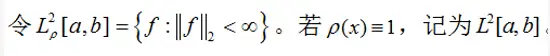
如果空间 Φ\Phi 是空间 Lρ2[a,b]L^2_{\rho}[a,b] 的子空间，那么空间 Φ\Phi 中的函数 s(x)s(x) 可以记为：

接下来开始正式地描述最佳平方逼近问题，最佳平方逼近函数的定义如下所示，如前所述，函数f 所处的空间 L^2_{\rho}[a,b] 更大，而函数 s 所处的空间 \Phi更小，最佳平方逼近所做的事情是用一个低维空间的函数去逼近高维空间的函数，使得他们之间的平方误差最小。

最佳平方逼近问题的直观描述如下图所示：

接下来的问题是如何求解这个最佳平方逼近函数 s^* ，因为 s^*(x) 是 \varphi(x) 的线性组合，而需要确定的只是 \varphi(x)前的系数，而需要去逼近的函数f(x) 是已知的，显然这就是一个求函数极值的问题，把待定系数当做自变量，而其他的部分当做已知量，求这个函数的极值，即：

多元函数 F能取到极值的必要条件是对各个自变量的偏导数为0，即：

将函数 F 的表达式代入后整理即得（其中用了一个小技巧就是求导和积分符号互换位置）：

由上图可知，法方程给定了待定系数 a_j 的值，从而最佳平方逼近函数 s^*(x)就得到了求解。将上述法方程整理成矩阵的形式即为：

由于 \varphi_j(x) 是空间 L^2_{\rho}[a,b] 的一组基，所以最佳平方逼近函数 s^*(x) 的解唯一，即：

需要注意的是，虽然证明了 s^*(x) 的存在性和唯一性，但 s^*(x) 未必能使 F 取得最小值，因为偏导数为0只是必要条件，并不是充分条件，下面还需要证明它能使 F 取得最小值。

下面这张图给出了证明思路，只要证明 f-s^* 与空间 \Phi 中的任一函数 s 正交，那么就可以证明 ||f-s^*|| \leq||f-s||

根据法方程可知：

上式也就说明了 f-s^* 与空间 \Phi 中的所有基函数正交，从而也就说明了与与空间 \Phi 中的任意函数正交。从而证明就结束了， ||f-s^*|| 即为 ||f-s|| 的最小值。以上是从几何的角度给出的证明，用代数的角度给出证明如下：

逼近的误差称为最佳平方逼近误差，即：

对于最佳平方逼近函数，来考虑一种特殊的情况，即空间 \Phi是多项式函数组成的空间：

相应的待定系数可以通过法方程求解，即：

遗憾的是，虽然这个 \Phi 空间的基足够简单，但是Hilbert矩阵是病态的，想要通过这个矩阵求解系数 a^*_j非常困难。因此为了简化法方程，通常采用Gram-Schemidt 方法将\Phi 空间的基转换为正交基，从而法方程的系数矩阵会变为一个对角矩阵，从而最佳平方逼近函数 s^*(x) 可以写为：

上式中要求 \varphi_j(x) 是 \Phi空间的正交基。