数值分析：三、逼近与拟合

 

本文并非对数值分析进行专业的介绍，而是学习计算机图形学的数学笔记，主要参考清华大学出版《数值分析》第五版，在内容上有所取舍。

复杂函数的函数值往往不能直接求解，所以我们需要构造一个便于计算的简单函数，并使这个函数尽量的逼近原函数，从而通过计算简单函数的函数值近似原函数函数值。上一章介绍了用插值法近似f(x)f(x) ，这里介绍逼近法和拟合法近似 f(x)f(x) 。这三种方法有相似之处，也有不同之处。

插值法，通常只已知函数的点列(xi,f(xi)),i=0,1,2,⋯,n(x_i,f(x_i)),\ i=0,1,2,\cdots,n ，构造简单函数 S(x)S(x) 经过所有点列，即 S(xi)=f(xi)S(x_i) = f(x_i) 。我常用多项式插值函数 f(x)f(x) ，用三角多项式插值周期函数 f(x)f(x) 。

逼近法，通常已知函数 f(x)f(x) 的形式，构造简单函数 S(x)S(x) ，使得 ||S(x)−f(x)||||S(x)-f(x)|| 在区间 [a,b][a,b] 上尽可能小 。我常用多项式逼近函数 f(x)f(x) ，用三角多项式逼近周期函数 f(x)f(x) 。

拟合法，通常只已知函数的点列 (xi,f(xi)),i=0,1,2,⋯,n(x_i,f(x_i)),\ i=0,1,2,\cdots,n ，构造简单函数 S(x)S(x) ，使得 ||S(x)−f(x)||||S(x)-f(x)|| 在区间 [a,b][a,b] 上尽可能小 。我常用多项式拟合函数 f(x)f(x) ，用三角多项式拟合周期函数 f(x)f(x) 。

逼近法和拟合法具有相似之处，也即构造 S(x)S(x) ，使得 f(x)f(x) 与 S(x)S(x)的误差在某种度量意义下最小。由万能逼近定理可知，这种近似函数的存在。

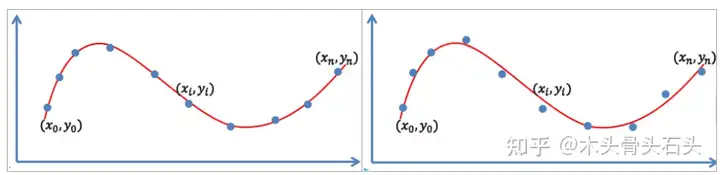
插值法和拟合法具有相似之处，也即它们都仅知道函数的点列 (xi,f(xi)),i=0,1,2,⋯,n(x_i,f(x_i)),\ i=0,1,2,\cdots,n ，在用三角多项式拟合点列 (xi,f(xi)),i=0,1,2,⋯,n(x_i,f(x_i)),\ i=0,1,2,\cdots,n 时，当三角多项式的项数 m=nm = n，那么最佳拟合三角多项式就是插值三角多项式

左图插值，右图拟合

之前在向量的内积与内积空间中提到了，在数值分析中，常用正交函数族作函数的逼近，所以需要先明确一下函数的内积，和正交函数的概念。

1 函数的逼近问题

万能逼近定理（Weierstrass 逼近定理）：对[a,b][a,b] 上的任意连续函数 gg ，及任意给定的 0">ε>0\varepsilon > 0 ，必存在 nn 次代数多项式： f(x)=∑i=0naixif(x) = \sum^n_{i=0} a_ix^i ，使得

从复平面上可以直观看到，当复数的模不变时，幅角旋转一个周期复数点回到原来的位置，幅角旋转半个周期复数点关于原点中心对称。

为了利用复数的周期性和对称性优化算法，要求 f(x)f(x) 已知的点 xjx_j 之间是等距的，其将一个一个周期等分成 N=2p,p=1,2,⋯N=2^p,\ p=1,2,\cdots 份。

快速傅里叶变换并未提出任何新的理论，只是提供了一种低复杂度的算法，能利用计算机更快速完成离散傅里叶变换及其逆变换。