简单函数列逼近可测函数是一直逼近吗？

在討論 函數逼近 的時候，要區分清楚它是以下何種逼近

而這個性質一開始先要求逐點收斂。 假設 f(x)f(x)的取值都在 0 到 1 之間，如下圖，那麼可以把落在下半部 (0 到 1/2 間) 和上半部 (1/2 至 1)的部份分別挑出來。

下半部取成 0、上半部取成 1，如下圖

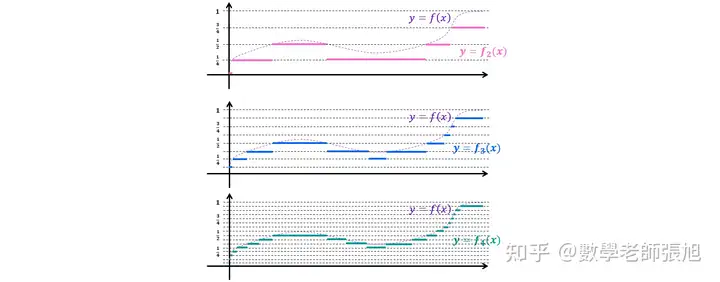
因此得到 f1(x)f_1(x) 。可再細分，因此會得到 f2(x),f3(x),f4(x)f_2(x), f_3(x),f_4(x) ,....。易知這樣做對每個點 x 而言 fn(x)→f(x)f_n(x)\to f(x)都會成立，所以它是逐點收斂。甚至可以證明它是一致收斂，因為在fn(x)f_n(x) 上面，構造方式已經確保了 |fn(x)−f(x)|≤12n|f_n(x)-f(x)|\leq \frac{1}{2^n} 。

接下來可以討論無界函數以及把正式的寫法寫出來了。若f:E→Rf:\mathbf E\to \mathbb R ，滿足 f(x)≥0f(x)\geq 0 ，則造