当深度学习遇上量化交易——模型篇

 

本文介绍三篇从模型层面着手解决股价预测问题的顶会文章。

Enhancing Stock Movement Prediction with Adversarial TrainingStock Price Prediction via Discovering Multi-Frequency Trading PatternsA Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction

1 Enhancing Stock Movement Prediction with Adversarial Training (IJCAI 2019)

众所周知，股票市场具有噪声高和随机性强的特点，传统使用静态历史数据训练的模型很容易过拟合。为了提高模型的泛化能力，文章提出通过对数据增加扰动来解决这一问题。其最大的亮点就是提出了使用对抗训练（Adversarial Training）的方式来训练模型。

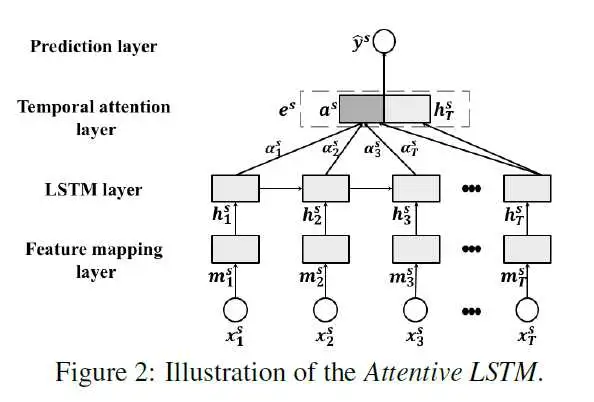
首先，为了适应股票数据时序依赖的特点，文章首先提出了Attentive LSTM。为了预测某一时刻的股价走势（1代表上涨，0代表下跌），输入之前TT天的数据Xs=[x1s,⋯,xTs]∈RD×T\boldsymbol{X}^{s}=\left[\boldsymbol{x}_{1}^{s}, \cdots, \boldsymbol{x}_{T}^{s}\right] \in \mathbb{R}^{D \times T}。之后输入一个全连接层获取特征的隐向量：

mts=tanh⁡(Wmxts+bm)\boldsymbol{m}_{\boldsymbol{t}}^{\boldsymbol{s}}=\tanh \left(\boldsymbol{W}_{\boldsymbol{m}} \boldsymbol{x}_{\boldsymbol{t}}^{\boldsymbol{s}}+\boldsymbol{b}_{\boldsymbol{m}}\right) \\

之后使用LSTM捕捉时序依赖，获得隐向量[h1s,⋯,hTs]∈RU×T\left[\boldsymbol{h}_{1}^{s}, \cdots, \boldsymbol{h}_{T}^{s}\right] \in \mathbb{R}^{U \times T}， 因为不同时间的状态对时刻TT的股价走势影响是不同的，使用时序注意力层（Temporal Attention Layer）来对隐向量进行加权求和：

as=∑t=1Tαtshts,αts=expα~ts∑t=1Texpα~tsα~ts=uaTtanh⁡(Wahts+ba)\begin{array}{l} \boldsymbol{a}^{s}=\sum_{t=1}^{T} \alpha_{t}^{s} \boldsymbol{h}_{t}^{s}, \quad \alpha_{t}^{s}=\frac{e x p^{\widetilde{\alpha}_{t}^{s}}}{\sum_{t=1}^{T} \exp ^{\widetilde{\alpha}_{t}^{s}}} \\ \widetilde{\alpha}_{t}^{s}=\boldsymbol{u}_{a}^{T} \tanh \left(\boldsymbol{W}_{a} \boldsymbol{h}_{t}^{s}+\boldsymbol{b}_{a}\right) \end{array} \\

之后将时刻TT的隐向量和加权求和的结果拼接获取最终的股票表示，计算获取预测结果：

es=[asT,hTsT]Te^{s}=\left[a^{s T}, h_{T}^{s T}\right]^{T} \\y^s=sign(wpTes+bp)\hat{y}^{s}=sign(\boldsymbol{w}_{p}^{T} \boldsymbol{e}^{s}+b_{p}) \\

但这种训练方式不那么适用于股票市场，因为我们输入模型的数据（如各种技术因子的取值）是有随机性的，因此很容易导致过拟合而缺少泛化性能。而一个好的模型应当能捕捉随机性。所以文章提出了对抗训练的方式。

首先来思考一个问题，怎么提高模型建模随机性的能力？自然的想法就是如果我们对输入样本加一个扰动，模型仍然可以正确预测，那么模型肯定能很好的抵御随机性。那么这个扰动怎么加也很有学问，我们希望加的扰动能够让模型输出结果发生最大的改变。那么哪个方向的扰动能够让模型输出结果发生最大的改变呢？回忆一下梯度下降法，梯度方向是下降最快的方向。显然，样本的梯度方向就是我们寻求的那个能够让模型输出结果发生最大改变的方向。所以从本质上来说，文章提出的对抗训练就是一种梯度下降法，不过梯度下降法优化的是参数，而这里的对抗训练改变的是样本，得到对抗样本。

根据上图所示，生成对抗样本的计算过程如下：

eadvs=es+radvse_{a d v}^{s}=e^{s}+r_{a d v}^{s} \\radvs=ϵgs‖gs‖,gs=∂l(ys,y^s)∂es\boldsymbol{r}_{a d v}^{s}=\epsilon \frac{\boldsymbol{g}^{s}}{\left\|\boldsymbol{g}^{s}\right\|}, \boldsymbol{g}^{s}=\frac{\partial l\left(\boldsymbol{y}^{s}, \hat{y}^{s}\right)}{\partial \boldsymbol{e}^{s}} \\l(ys,y^s)=max(0,1−ysy^s)l\left(y^{s}, \hat{y}^{s}\right)=\max \left(0,1-y^{s} \hat{y}^{s}\right) \\

其中ese^{s}是原样本。之后将对抗样本的训练和损失也加入到目标函数中：

Γadv=∑s=1Sl(ys,y^s)+β∑s=1Sl(ys,y^advs)+α2‖Θ‖F2\Gamma_{a d v}=\sum_{s=1}^{S} l\left(y^{s}, \hat{y}^{s}\right)+\beta \sum_{s=1}^{S} l\left(y^{s}, \hat{y}_{a d v}^{s}\right)+\frac{\alpha}{2}\|\Theta\|_{F}^{2} \\

模型的总体结构如下：

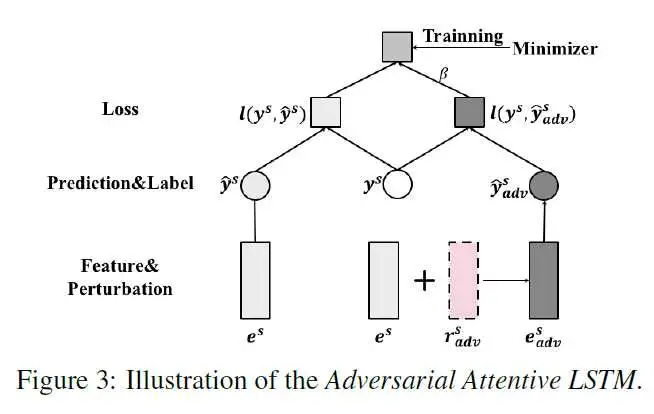
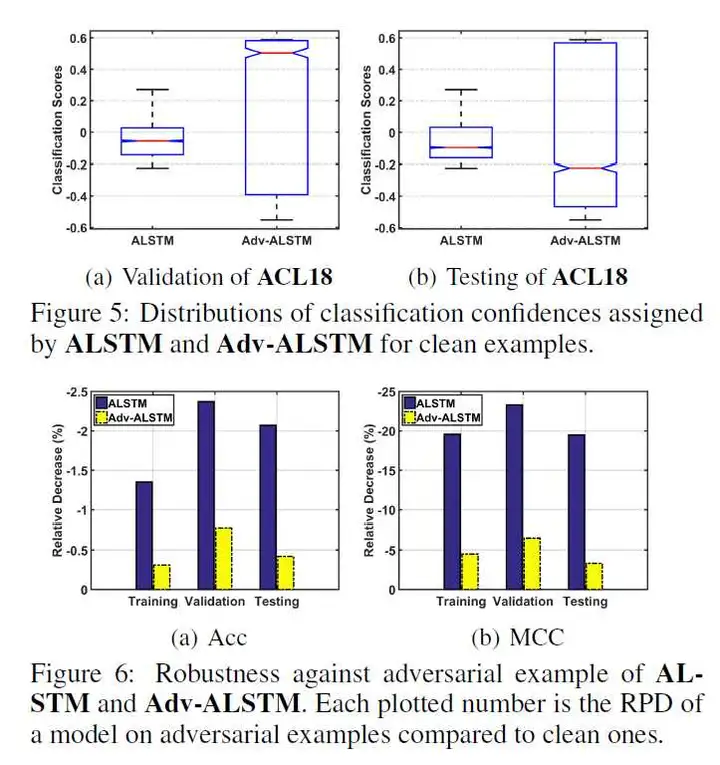
文章在ACL18和KDD17两个数据集上进行了实验，结果证明方法了有效性，同时与ALSTM的对比实验表明，使用对抗样本训练的模型分类置信度更高，扩展了决策边界，增强了模型的鲁棒性和泛化性能。

2 Stock Price Prediction via Discovering Multi-Frequency Trading Patterns (KDD 2017)

这是一篇应用的文章，作者还发了一篇偏理论的文章在ICML 2017上：State-Frequency Memory Recurrent Neural Networks, in Proceedings of International Conference on Machine Learning。我们通常使用LSTM来建模时间序列之间的长期依赖。如果我们将股价的变动看作一种信号处理任务的话，那么利用LSTM来预测股价变动只捕捉了时域上的信息，而忽略了频域上的信息。而对于股价信号来说，频域上的信息是非常有用的，其中的高频部分反应了股价的波动性，低频部分捕捉了长期的趋势和规律。基于此，文章提出了SFM来同时建模时间序列的时域与频域信息。

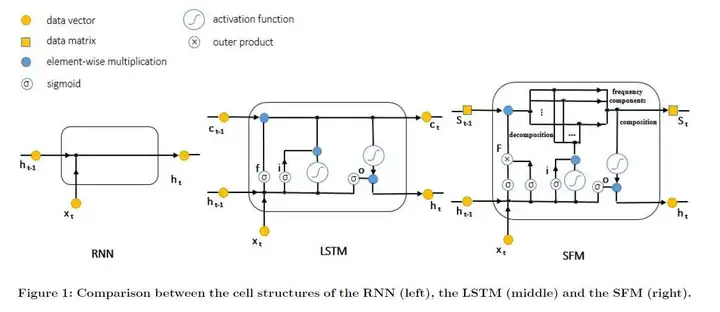
传统的LSTM结构大家都知道，这里不再赘述。我们来介绍下文章提出的SFM对于传统LSTM的三个改进：

将LSTM中的记忆细胞CtC_t变成状态-频率矩阵(the state-frequency matrix)StS_t将遗忘门改成联合状态-频率遗忘门利用傅里叶变换和逆变换使信号能够在时域与频域之间转换。

对于时间步tt，模型有三个输入：数据xtx_t、上一时间步的状态-频率矩阵St−1S_{t-1}、上一时间步的隐向量(hidden state)ht−1h_{t-1}, 后两者开始时初始化为0。状态-频率矩阵是一个DD行KK列的矩阵，每一列可以看作多个状态，每个状态在物理意义上可以理解成代表某个引发信号波动的因子；矩阵中的一行可以看作某状态的各个频率组件的权重。

因为每个时间步传递的是状态-频率矩阵，所以遗忘门被分为状态遗忘门(state forget gate)ftstef_{t}^{s t e}和频率遗忘门(frequency forget gate)ftfref_{t}^{fre}：

ftste=sigmoid⁡(Wstext+Usteht−1+bste)∈RDftfre=sigmoid⁡(Wfrext+Ufreht−1+bfre)∈RK\begin{aligned} f_{t}^{s t e} &=\operatorname{sigmoid}\left(\boldsymbol{W}_{s t e} \boldsymbol{x}_{t}+\boldsymbol{U}_{s t e} \boldsymbol{h}_{t-1}+\boldsymbol{b}_{s t e}\right) \in \mathbb{R}^{D} \\ f_{t}^{f r e} &=\operatorname{sigmoid}\left(\boldsymbol{W}_{f r e} \boldsymbol{x}_{t}+\boldsymbol{U}_{f r e} \boldsymbol{h}_{t-1}+\boldsymbol{b}_{f r e}\right) \in \mathbb{R}^{K} \end{aligned} \\

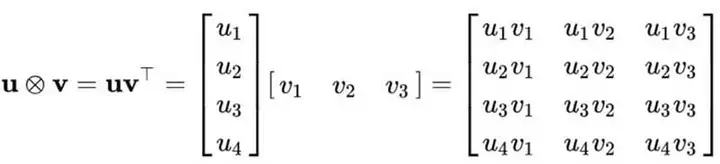
利用外积操作⊗\otimes（运算规则如上图所示）将两个遗忘门联合成状态-频率遗忘门FtF_{t}:

Ft=ftste⊗ftfre∈RD×K\boldsymbol{F}_{t}=\boldsymbol{f}_{t}^{s t e} \otimes \boldsymbol{f}_{t}^{f r e} \in \mathbb{R}^{D \times K} \\

输入门iti_t和输入调制(input modulation)c~t\tilde{c}_{t}和LSTM保持一致：

it=sigmoid⁡(Wixt+Uiht−1+bi)c~t=tanh⁡(Wcxt+Ucht−1+bc)\begin{array}{l} i_{t}=\operatorname{sigmoid}\left(W_{i} x_{t}+U_{i} h_{t-1}+b_{i}\right) \\ \tilde{c}_{t}=\tanh \left(W_{c} x_{t}+U_{c} h_{t-1}+b_{c}\right) \end{array}\\

对于状态-频率矩阵的更新操作向量计算形式如下：

St=Ft∘St−1+(it∘c~t)[ejω1tejω2t…ejωKt]T∈CD×KS_{t}=F_{t} \circ S_{t-1}+\left(i_{t} \circ \tilde{c}_{t}\right)\left[\begin{array}{c} e^{j \omega_{1} t} \\ e^{j \omega_{2} t} \\ \ldots \\ e^{j \omega_{K} t} \end{array}\right]^{T} \in \mathbb{C}^{D \times K}\\

其中j=−1j=\sqrt{-1}， [ejω1t,ejω2t,…,ejωKt]\left[e^{j \omega_{1} t}, e^{j \omega_{2} t}, \ldots, e^{j \omega_{K} t}\right]是KK个频率部分的傅立叶基函数。∘\circ是按元素乘。

现在已经有了当前时间步的状态-频率矩阵StS_{t}，之后要更新当前时间步的隐藏状态hth_t。首先利用欧拉公式eix=cos⁡x+isin⁡xe^{i x}=\cos x+i \sin x把StS_{t}的更新公式分为实部和虚部两部分：

Re⁡St=Ft∘Re⁡St−1+(it∘ct~)[cos⁡ω1t,…cos⁡ωKt]Im⁡St=Ft∘Im⁡St−1+(it∘ct~)[sin⁡ω1t,…sin⁡ωKt]\begin{aligned} \operatorname{Re} \boldsymbol{S}_{t} &=\boldsymbol{F}_{t} \circ \operatorname{Re} \boldsymbol{S}_{t-1}+\left(\boldsymbol{i}_{t} \circ \tilde{\boldsymbol{c}_{t}}\right)\left[\cos \omega_{1} t, \ldots \cos \omega_{K} t\right] \\ \operatorname{Im} \boldsymbol{S}_{t} &=\boldsymbol{F}_{t} \circ \operatorname{Im} \boldsymbol{S}_{t-1}+\left(\boldsymbol{i}_{t} \circ \tilde{\boldsymbol{c}_{t}}\right)\left[\sin \omega_{1} t, \ldots \sin \omega_{K} t\right] \end{aligned} \\

此外，复数可以表示成振幅AtA_{t}和相位∠St\angle S_{t}：

At=|St|=(ReSt)2+(ImSt)2∈RD×K∠St=arctan⁡(ImStReSt)∈[−π2,π2]D×K\begin{aligned} A_{t} &=\left|S_{t}\right|=\sqrt{\left(R e S_{t}\right)^{2}+\left(I m S_{t}\right)^{2}} \in \mathbb{R}^{D \times K} \\ \angle S_{t} &=\arctan \left(\frac{I m S_{t}}{R e S_{t}}\right) \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]^{D \times K} \end{aligned}\\

但后面的计算只用到了振幅AtA_{t}，因为实验证明相位∠St\angle S_{t}对结果没有显著影响。利用振幅信息获取记忆状态：

ct=tanh⁡(Atua+ba)c_{t}=\tanh \left(A_{t} u_{a}+b_{a}\right) \\

上述过程可以被看做是傅立叶逆变换，但比起标准的傅立叶逆变换，文章选择可训练权重uau_{a}来适应训练任务。之后的更新过程与LSTM一致：

ot=sigmoid⁡(Woxt+Uoht−1+Voct+bo)ht=ot∘ct\begin{array}{l} \boldsymbol{o}_{\boldsymbol{t}}=\operatorname{sigmoid}\left(\boldsymbol{W}_{\boldsymbol{o}} \boldsymbol{x}_{\boldsymbol{t}}+\boldsymbol{U}_{\boldsymbol{o}} \boldsymbol{h}_{\boldsymbol{t}-1}+\boldsymbol{V}_{\boldsymbol{o}} \boldsymbol{c}_{\boldsymbol{t}}+\boldsymbol{b}_{\boldsymbol{o}}\right) \\ \boldsymbol{h}_{\boldsymbol{t}}=\boldsymbol{o}_{\boldsymbol{t}} \circ \boldsymbol{c}_{\boldsymbol{t}} \end{array} \\

文章使用2007到2014年的50只股票的股价数据作为训练集，2015年的数据作为验证集，2016年的数据作为测试集进行了实验，SFM在预测1天后、3天后、5天后的股价均表现最佳：

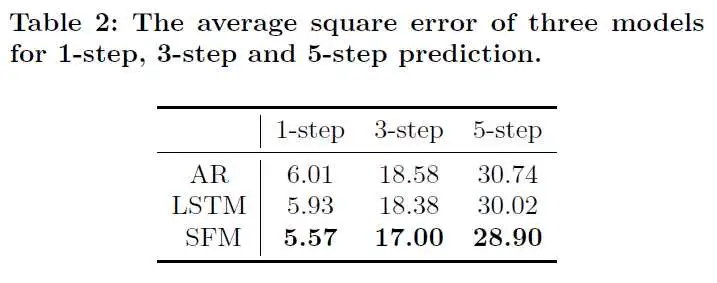
此外，文章探索了时间窗口ww、状态数量DD、频率数量KK三个参数的影响，结论如下：

AR的表现会随着ww的增大而变差，LSTM与SFM则会变好。证明了LSTM和SFM对于长期依赖的捕捉能力对于短期预测，太多的状态会让结果变差（过拟合），而长期预测则需要更多的状态来提供更多信息短期预测需要更多的频率成分来表现短期股价的高波动性，而长期预测则依赖于那些比较稳定的低频成分。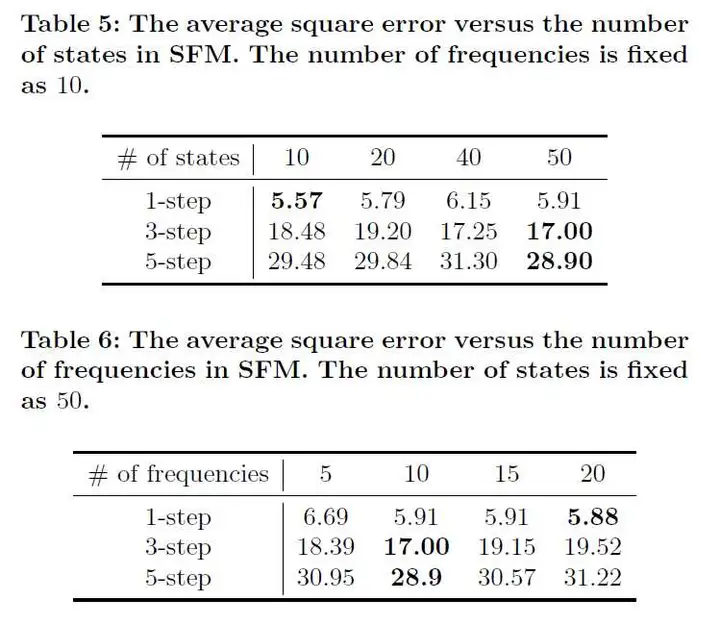

3 A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction(IJCAI 2017)

上一篇文章改造LSTM来进行股市预测，这篇文章则提出一种变种的Seq2Seq模型DA-RNN来进行端到端的时序预测任务。模型结构比较简单，如下图所示：

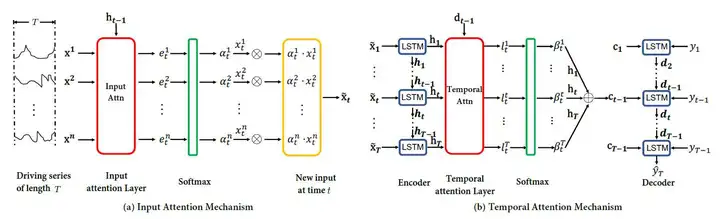
相比于传统的Seq2Seq模型，DA-RNN在输入端增加了一个input attention层。可以分成两部分：Encoder with input attention、Decoder with temporal attention。

编码器部分，在时间步tt，输入有当前时间步的特征xt=(xt1,xt2,⋯,xtn)⊤∈Rn\mathbf{x}_{t}=\left(x_{t}^{1}, x_{t}^{2}, \cdots, x_{t}^{n}\right)^{\top} \in \mathbb{R}^{n}, 上一时间步获得的隐状态ht−1h_{t-1}和记忆细胞cst−1cs_{t-1}，首先输入Input attention Layer获取对每个特征的加权x~t\tilde{\mathbf{x}}_{t}:

etk=ve⊤tanh⁡(We[ht−1;st−1]+Uextk)e_{t}^{k}=\mathbf{v}_{e}^{\top} \tanh \left(\mathbf{W}_{e}\left[\mathbf{h}_{t-1} ; \mathbf{s}_{t-1}\right]+\mathbf{U}_{e} \mathbf{x_t}^{k}\right) \\αtk=exp⁡(etk)∑i=1nexp⁡(eti)\alpha_{t}^{k}=\frac{\exp \left(e_{t}^{k}\right)}{\sum_{i=1}^{n} \exp \left(e_{t}^{i}\right)} \\x~t=(αt1xt1,αt2xt2,⋯,αtnxtn)⊤\tilde{\mathbf{x}}_{t}=\left(\alpha_{t}^{1} x_{t}^{1}, \alpha_{t}^{2} x_{t}^{2}, \cdots, \alpha_{t}^{n} x_{t}^{n}\right)^{\top} \\

之后输入作为编码器的LSTM获得当前时间步的隐状态hth_{t}:

ht=LSTM(ht−1,x~t)\mathbf{h}_{t}=\text{LSTM}\left(\mathbf{h}_{t-1}, \tilde{\mathbf{x}}_{t}\right) \\

解码器的结构与带Attention的Seq2Seq一致，只不过这里的Attention改叫temporal attention，对于时间步tt，解码器能够获得编码器输出的隐向量hi,1≤i≤Th_i,1 \leq i \leq T， 上一时间步的解码器隐向量dt−1∈Rp\mathbf{d}_{t-1} \in \mathbb{R}^{p}，记忆细胞状态st−1′∈Rp\mathbf{s}_{t-1}^{\prime} \in \mathbb{R}^{p}， 上一时间步的真实标签yt−1y_{t-1}。给编码器的隐向量赋予不同的注意力权重，计算当前时间步的情景(context)向量：

lti=vd⊤tanh⁡(Wd[dt−1;st−1′]+Udhi),1≤i≤Tl_{t}^{i}=\mathbf{v}_{d}^{\top} \tanh \left(\mathbf{W}_{d}\left[\mathbf{d}_{t-1} ; \mathbf{s}_{t-1}^{\prime}\right]+\mathbf{U}_{d} \mathbf{h}_{i}\right), \quad 1 \leq i \leq T \\βti=exp⁡(lti)∑j=1Texp⁡(ltj)\beta_{t}^{i}=\frac{\exp \left(l_{t}^{i}\right)}{\sum_{j=1}^{T} \exp \left(l_{t}^{j}\right)} \\ct=∑i=1Tβtihi\mathbf{c}_{t}=\sum_{i=1}^{T} \beta_{t}^{i} \mathbf{h}_{i} \\

将上一时间步的真实标签yt−1y_{t-1}和情景向量拼接成当前时间步的解码器输入：

y~t−1=w~⊤[yt−1;ct−1]+b~\tilde{y}_{t-1}=\tilde{\mathbf{w}}^{\top}\left[y_{t-1} ; \mathbf{c}_{t-1}\right]+\tilde{b} \\

同样采用LSTM作为解码器，获取当前时间步的解码器隐状态dtd_{t}：

dt=LSTM(dt−1,y~t−1)\mathbf{d}_{t}=\text{LSTM}\left(\mathbf{d}_{t-1}, \tilde{y}_{t-1}\right) \\

之后可以预测时刻TT的输出：

y^T=F(y1,⋯,yT−1,x1,⋯,xT)=vy⊤(Wy[dT;cT]+bw)+bv\begin{aligned} \hat{y}_{T} &=F\left(y_{1}, \cdots, y_{T-1}, \mathbf{x}_{1}, \cdots, \mathbf{x}_{T}\right) \\ &=\mathbf{v}_{y}^{\top}\left(\mathbf{W}_{y}\left[\mathbf{d}_{T} ; \mathbf{c}_{T}\right]+\mathbf{b}_{w}\right)+b_{v} \end{aligned}\\

文章选取了SML 2010和NASDAQ 100两个数据集进行实验。实验表明文章提出的DA-RNN更适合时序预测任务。

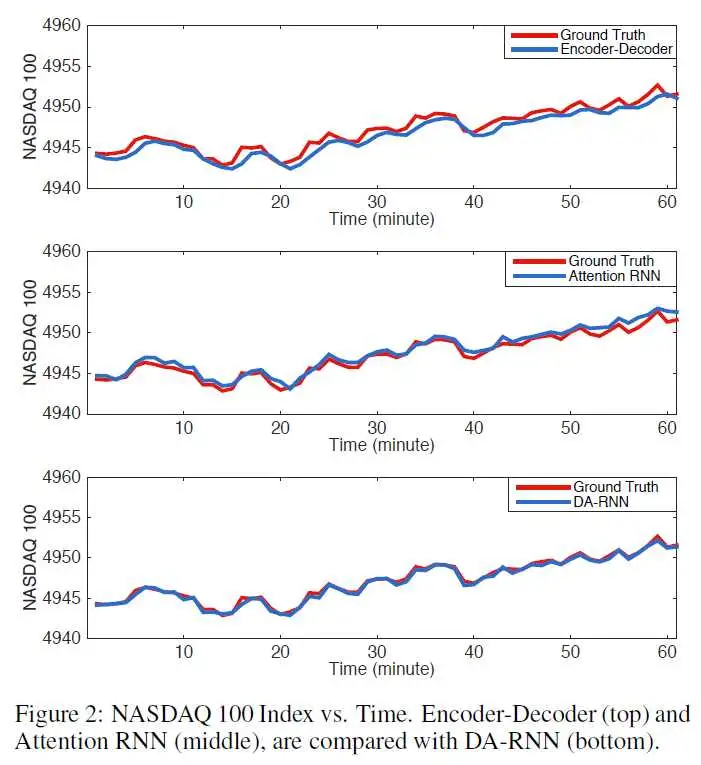
文章还将模型的输入做了扰动后拼接上正常的输入进行训练，发现input attention对于扰动后的数据赋予了较低的权重，证明了input attention让模型抗干扰能力更强。此外，文章对模型参数时间窗口TT和LSTM隐层大小mm进行了测试，在NASDAQ 100 Stock上的最优参数是T=10,m=64T=10, m=64。

总结

股价数据具有极低信噪比、随机性强、时序依赖的特点，比一般的序列预测任务相比更加困难，模型改进的方向也是尽可能的提升模型的抗干扰能力（对抗训练），从噪声中提取有价值的信号（频域、注意力机制）。希望未来在这一领域看到更多更有创造性的工作。