什么是量化交易的Barra多因子模型？

网上的文章主要两个版本吧，一个是翻译Barra，纯翻译，不解释，二是大神太多，根本不屑于解释很多结论是如何来的，就算大家把各种文章看完，也只是似是而非的懂了。

本文为系列文，今天这篇解释了Barra模型为什么会出现，是解决什么实际问题，然后推导一个最基础的Barra模型。

一、为什么会有Barra模型？

学过资产组合投资这门课的盆友，肯定对一个模型不陌生，这个模型就是Markowitz均值-方差模型，这个模型的特点呢就是通过各种资产组合分散风险，寻找风险最小化，而收益最大化的模型。然后可以画出下面这个曲线，在给定的标准差（横坐标，风险）情况下，我们可以找到一个对应的期望收益（投资收益）最大的点。

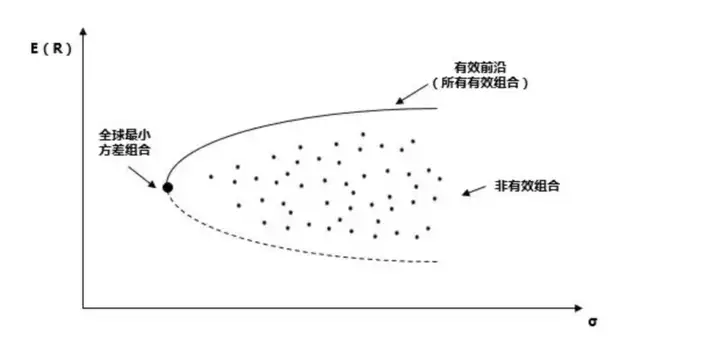
但是这种刻画风险和收益的方式：

（1）需要计算全市场股票与股票之前的相关性，比如A股有5000只股票，我们就需要计算股票A和另外4999只股票的协方差矩阵：

因为这个矩阵是对称矩阵，我们仅需要计算一半的数，依然需要计算5000 * 5001 / 2 次！

（2）我们一般会选取一段历史数据比如说252天的收益率滚动计算股票的相关性，但是股票的数量远远大于252，在数学中我们这个协方差矩阵不满秩，不存在逆方差矩阵，这样我们在实际中无法使用一些估计方法。想具体了解的看这篇文章就够了：https://zhuanlan.zhihu.com/p/355241680

所以Barra模型很好的解决了上述两个问题，假设股票个数为N，Barra因子的个数为n，Barra模型将我们需要计算N*（N+1）/2 次数的模型，降到了只需要计算n * (n + 1) / 2 + n 次，因为因子个数n很少，所以我们也不用担心上述（2）的问题。

前面说到Barra模型的基础就是认为股票的收益是由一些共同的因子来驱动的，所以假设现在市场上有K个驱动股票收益的因子，那么Barra模型的表示为：

其中：

ri代表股票i的收益率

Xik代表股票在k因子的暴露程度，也叫因子载荷，其实这个东西就是k因子对股票i收益的贡献度有多少，无论什么名字，在股票中，比如说我们说计算价值因子的对股票收益率的贡献度，我们可以使用股票的BM值来作为Xik。

ui代表股票的特质性收益率，每个股票的特质性收益率是不一样的，是无法我们用我们上述的公共因子来解释的。

假设一个资产组合中有N只股票，股票i在组合中的权重为wi，组合的收益率可以表示为：

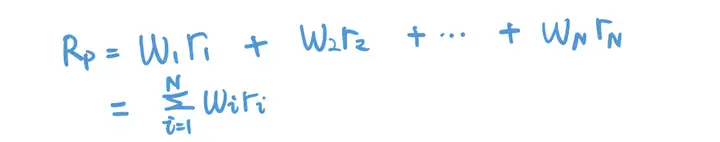
整个组合在因子k上的暴露程度就等于组合里所有股票在因子k上的暴露简单加和。

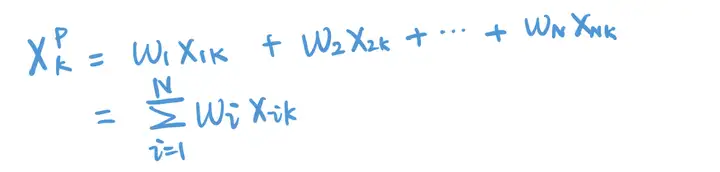
通过上述计算，我们可以按照下述流程，推导出Rp的新表达式：

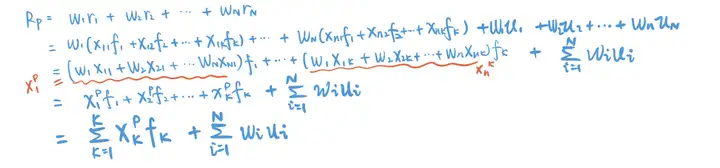
这个时候发现没有我们Barra多因子模型将描述组合收益率这件事直接降为了对K个因子的收益-风险分析。我们衡量组合风险的收益会用方差，所以我们再来推导一下方差，看看计算方差时候的时候计算量是多少。

在计算之前，Barra模型有两个假设：

（1）股票的特异性收益和因子解释的收益率之间是独立的，因此因子收益率和特异性收益率之间不存在协方差。（2）不同股票的特异性收益率是相互独立的，因此股票的特异性收益率的协方差也为 0。

在我们推导之前，先来复习一下方差的计算基础公式:

然后我们看到组合的方差，其实就被分为了两部分。

要计算我们组合的方差的第一部分，首先我们准备一个数学公式，如下：

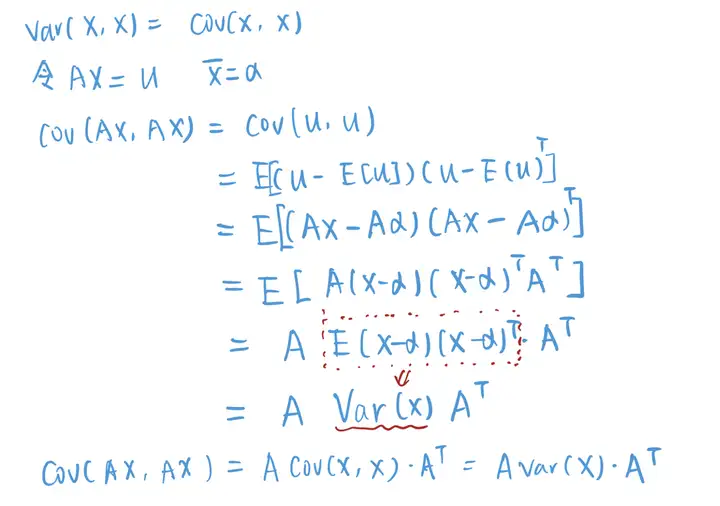
然后我们将组合的方差的第一部分转换为矩阵进行表达：

接着我们计算第二部分：

所以Barra最基本的模型到这里已经全部推导完毕，真的清晰，最后我们从推论出来的模型结果做一个总结

（1）从第一部分我们可以看出我们只需要求因子收益率向量的方差，也就是因子的协方差矩阵。所以我们的计算降为了计算k * （k+1） / 2，妥妥的降维

（2）Barra模型对组合风险的描述，也就拆分为了第一部分系统性风险，第二部分不能够被分散的风险。

（3）Barra模型在构建的时候要考虑两点：1是会不会遗漏到重要的因子，2是会不会因子冗余。

上周也做了版Brinson，放在知识星球了。