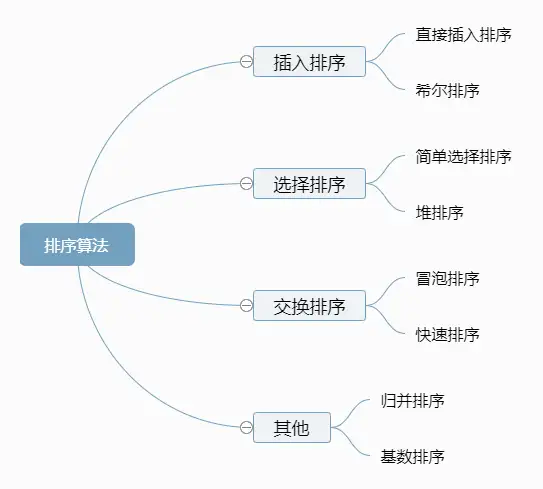
八大排序算法的关系如下:
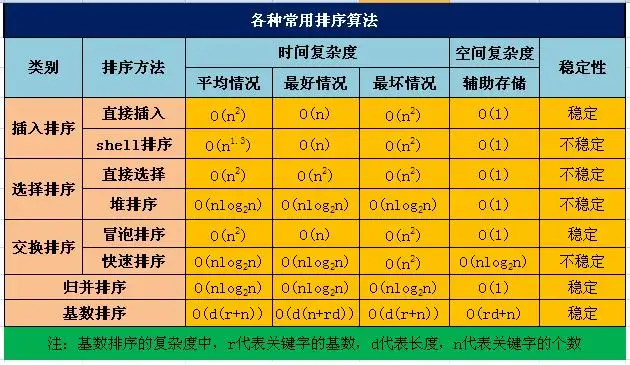
性能比较:
下面慢慢分析各大排序算法的原理实现和性能,慢慢来....不急, 一个一个来!!
直插排序
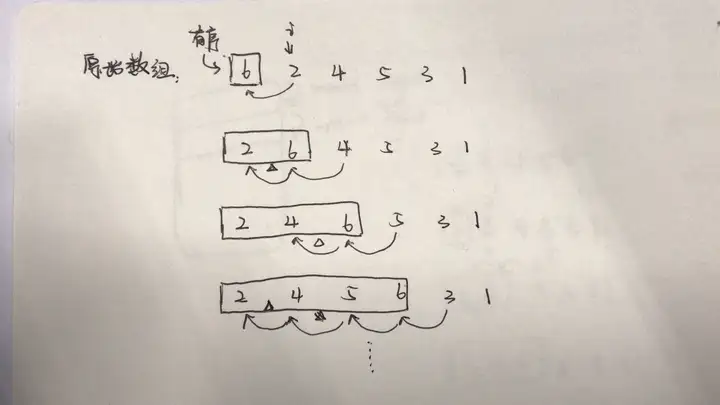
原理
对于第 i 个元素,其前面 i - 1 个元素已经有序,遍历前面的 i - 1 个有序元素,将这个元素插入到合适的的位置中,依次类推。
算法实现
public void insertSort(int[] arr) {
int len = arr.length;
for (int i = 1; i < len; i++) { // 从第二个元素开始,默认第一个已经有序
if (arr[i] < arr[i - 1]) { // 倒序遍历前 i - 1 个有序元素
int temp = arr[i];
for (int j = i - 1; j >= 0 & temp < arr[j]; j--) {
arr[j + 1] = arr[j]; // 依次往后挪动元素
}
arr[j + 1] = temp; // 插入位置
}
}
}
分析
① 最好情况:
元素全部有序,第个元素开始在遍历时都不会满足if (arr[i] < arr[i - 1]) 这个条件,因此只会进行 n - 1次比较,时间复杂度为O(n)。
② 最坏情况:
元素为逆序,需要比较次数为:1 + 2 + … + (n - 1) = n * (n - 1) / 2 次, 因此时间复杂度为O(n²)。
希尔排序
原理
希尔排序(Shell Sort)又叫缩小增量排序。
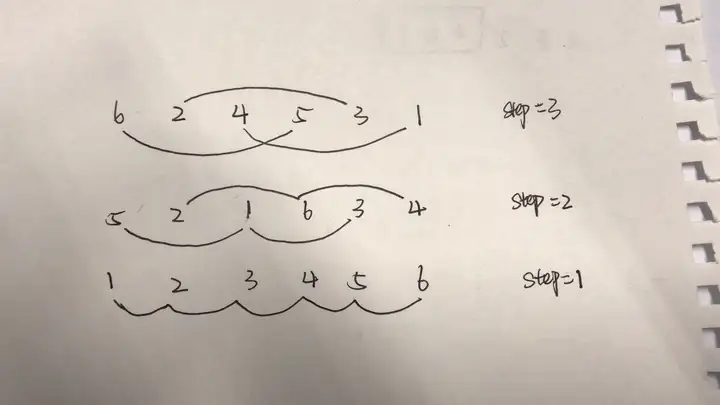
设定一个初始步长,对元素进行分组的插入排序,然后逐渐缩小步长,每缩小一次步长,就会对同组元素进行一次插入排序,直到步长为0。
好处:刚开始步长最大,需要插入排序的元素少,速度快;而步长很小时元素都基本有序了,需要挪动的元素少,速度快。
我们还需要知道的是,希尔排序是对直接插入排序的一个改进,可以理解成先分组再直插排序。
简单选择排序
原理
简单选择排序很简单…假设数组长度为n, 第一次从n个里面选择最小的数与arr[0]交换,第二次从后 n - 1 个数中选最小的与arr[1]交换... 以此类推。
算法实现
public void easySelectSort(int[] arr) {
int len = arr.length;
for (int i = 0; i < len; i++) {
int min = i;
for (int j = i + 1; j < len; j++) { // 找最小的元素下标 → min
if (arr[j] < arr[min]) {
min = j;
}
}
if (min != i) { // 交换
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
}
分析
由于简单选择排序算法每次都要遍历一次剩下的元素,然后决定交换问题,所以遍历这一步都是无法避免的。所以比较次数都为 (n - 1) + (n - 2) + … + 1 = n * (n - 1) / 2 → O(n²)。
所以最好和最坏情况都是一毛一样滴。
堆排序
原理
我们将原始数组抽象成一个堆的结构:
根据这个结构我们可以知道的是: 第 i 个结点其左右子节点分别是 arr[i * 2 + 1] 和 arr[i* 2 + 2],arr[0]为堆的根节点。
堆排序主要其实就是进行两步操作:1)构建大顶堆;2)通过选择和调整堆来构建有序的结果。
说起来有点抽象,我们直接上规则:
① 构建大顶堆
从第一个非叶子节点的点开始调整结点顺序,使其成为大顶堆。(第一个非叶节点为arr[len / 2 - 1])判断每一组(基准结点+其左右孩子节点)是否满足大顶堆结构,若不满足,则将最大孩子节点和基准结点交换重复上述步骤,直到构建为大顶堆
② 调整堆,使其成为有序数组
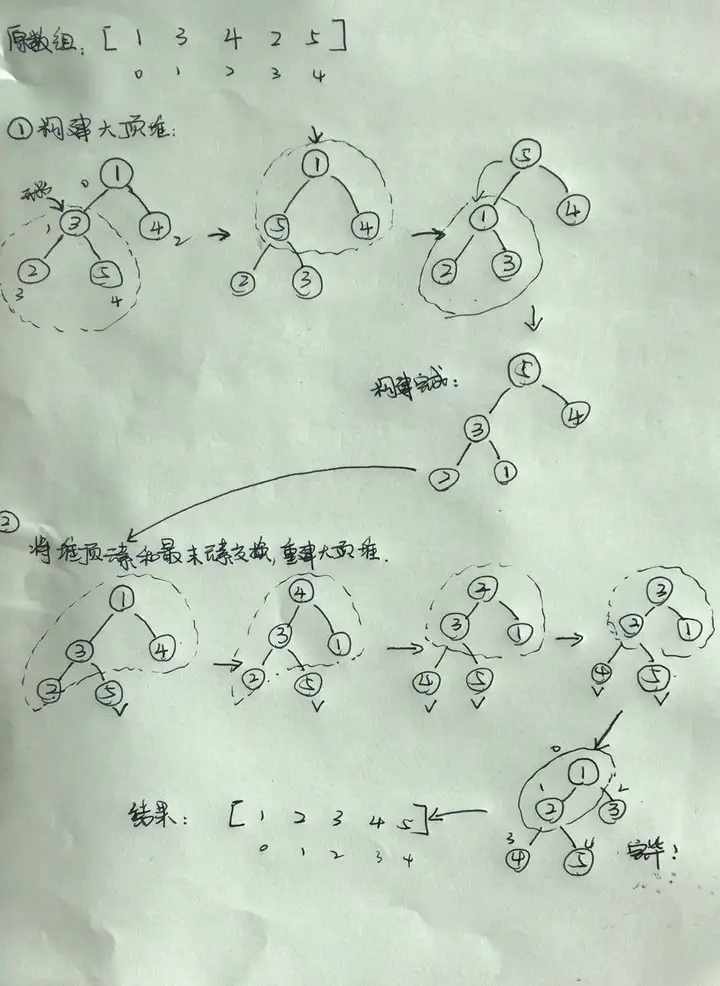
从最后一个节点开始,与根节点作交换交换后,忽略交换过的节点,调整剩余堆的结构,使其成为大顶堆重复以上步骤,直到所有元素交换完毕(这样能保证每一次交换后,最大的元素都换到下面去了)
放一张过程示意图:
算法实现
public void heapSort(int[] arr) {
int len = arr.length;
// ① 构建大顶堆
// 从第一个不是叶子节点的开始,从右到左,从上到下依次调整
for (int i = len / 2 - 1; i >= 0; i--) {
adjustNode(arr, i, len);
}
// ② 将大顶堆转换成有序数组过程 for (int i = len - 1; i > 0 ; i--) {
swap(arr, 0, i);
adjustNode(arr, 0, i);
}
}
/**
* arr: 数组
* base: 待调整的基准
* len: 数组长度 */
public void adjustNode(int[] arr, int base, int len) {
int originNum = arr[base];
// 从每一个结点的左下子节点开始,如有调整,则挪动元素并以被挪动的 // 子节点为基点,再重复以上过程。
for (int i = basse * 2 + 1; i < len; i = i * 2 + 1) {
if (i + 1 < len && arr[i + 1] > arr[i]) { // 如果右边的子节点大,则指向右边节点 i++;
}
if (arr[i] > arr[base]) { // 将大的那个子节点往上挪动,并将基准置为当前子节点
arr[base] = arr[i];
base = i;
} else { // 已经是大顶堆了 break;
}
}
}
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
冒泡排序
原理
冒泡排序的过程正如它的名字,像水里的气泡一样往上冒。
它能够保证每一趟都能把最小的元素移动到最前面去,具体过程是通过从后往前元素间两两比较,小的挪动到前面,依次类推向前操作。
再对之后 n - 1 个元素进行同样的操作,直到全部有序为止。
示意图:
算法实现
public void bubbleSort(int[] arr) {
int len = arr.length;
if (len == null || len == 0) return;
int swapCount; // 记录每一趟的交换次数
for (int i = 0; i < len - 1; i++) { // 只需要进行 n - 1 趟即可
if (swapCount == 0 && i != 0) { // 如果发现某一趟没有交换任何元素,证明已经有序 break;
}
swapCount = 0;
// 每进行完一趟,前i个元素已经有序
for (int j = len - 1; j > i; j--) {
if (arr[j] < arr[j - 1]) {
swap(arr, j, j - 1);
swapCount++;
}
}
}
}
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
分析
由于该算法的每一趟是从后往前依次比较交换的,如果在第一趟完成后,发现元素已经有序,则之后不需要再做后几趟的交换排序了,因此这种情况只需要比较 n - 1次,最好的时间复杂度为O(n);而最差情况下是做完每一趟的排序,因此总次数为 (n - 1) + (n - 2) + … + 1 = n * (n - 1) / 2,因此最坏时间复杂度为O(n²)。
快速排序
(未完待续...拼命更新中...)