干货！以点为形：可微分的泊松求解器

 

在过去的几年中，神经隐式表达因为其出色的表达能力以及灵活性而大受欢迎，但是它也受限于较慢的预测时间。在我们这篇文章里，我们重访了经典但强大的显式点云表达，并提出了一个可微分的泊松求解器，它可以高效的将有向的点云通过一个隐式的指示函数转化成稠密网格。 这样的点和网格之间的联系使得我们可以用简单，轻量并可解释的点云作为形状表达，这也使得预测时间相较于神经隐式表达加速了一个量级。同时相较于其他显示表达，我们又可以对各种不同拓扑的形状建模。最后，我们在基于纯优化以及基于深度学习的三维表面重建的任务上都表现出有效性。

本期AI TIME PhD直播间，我们邀请到苏黎世联邦理工学院 (ETH Zurich) 和德国马克思普朗克研究所智能系统所 (Max Planck Institute for Intelligent Systems)博士生——彭崧猷，为我们带来报告分享《以点为形：可微分的泊松求解器》。

彭崧猷：博士在读于苏黎世联邦理工学院 (ETH Zurich) 和德国马克思普朗克研究所智能系统所 (Max Planck Institute for Intelligent Systems)，由 Marc Pollefeys和Andreas Geiger共同指导。他的研究兴趣主要在三维视觉和深度学习的交叉，尤其感兴趣于研究三维场景的隐式和展示神经表达，以及它们在三维重建和神经渲染上的应用。

内容简介

对于任意物体的形状，我们可以表示为不同的形式。我们在本次研究中提出的SAP是经典泊松表面重建可微分的版本。除此之外，SAP也是一种新的物体形状表达方式。

那么什么是比较好的三维形状表达呢？

一些传统的形状表达方式早已经历了充足的研究，比如点云等。他们的优势是在inference的时候都非常高效，但是却普遍存在不连续的问题。

近几年有一个比较火的研究方向——Neural Implicit Representations，即可以把形状表达成网络的输出。但是却在inference中略慢。

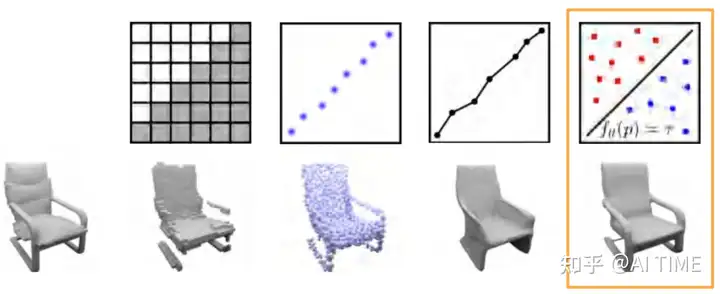
于是，我们提出了一种混合的表达形式。还是用点代表形状，但是我们把点和一个隐式的表达通过可微分的泊松求解器联系起来。一方面可以得到高品质的呈现，一方面可以很快的inference。

Method

可微分的泊松求解器DPSR：Differentiable Poisson Solver

上图左面是我们提供的带有法向量的定义域，泊松求解器可以从这个点云输出一个稠密的网格，并能够判断这个网格里的点是在物体内部还是外部。

对于求解泊松方程的关键，我们提供了二维的例子帮助理解。

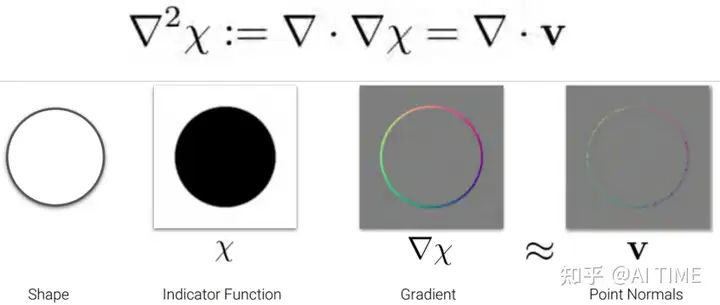
首先，我们考虑圆形作为我们的形状Shape，可以被转化成一个指示函数Indicator Function（黑色代表物体内部，白色代表物体外部），之后对其求导可以得到Gradient；发现只有在表面才存在导数；

当我们在表面sample一些点，同时知道法向量，就可以使得法向量和之前的指示函数建立联系。

求解泊松方程

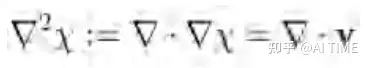
直接将散度算子求导，注意边界条件即可。

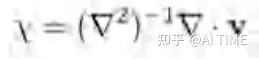
Spectral methods去求解泊松方程。

对信号在谱域的导数进行了解析计算快速傅里叶变换(FFT)在gpu / tpu上进行了高度优化只用了少量代码就可完成

我们提出的这个可微分的泊松求解器可以广泛应用到各种task上。

基于Unoriented Point云的三维表面重建（没有法向量）

1）SAP for Optimization-based 3D Reconstruction

纯优化的三维重建（没有深度学习网络）

在给定目标定云的情况下，恢复其三维模型。我们首先初始化一个带有法向量的点云，为了展示其灵活性和鲁棒性，我们从一个球去初始化出来点云和他的法向量。

然后我们可以把点云输入到DPSR泊松求解器去获得一个稠密的指示网格。

我们后续可以从网格中得到一个march，并从march上sample一些点；将这些点和target（目标点云）做一个tranfer distance得到loss。

我们便可以通过上述方法去update点云，

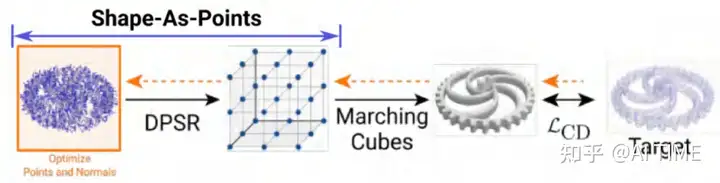
Comparison

我们可以发现我们的方法可以很好的恢复之前的形状。

之前经典的方法——泊松重建法如下图所示：

问题在于过于依赖法向量是否准确，一点的噪声就可能造成结果不准确。

2）SAP for Learning-based 3D Reconstruction（有深度学习网络）

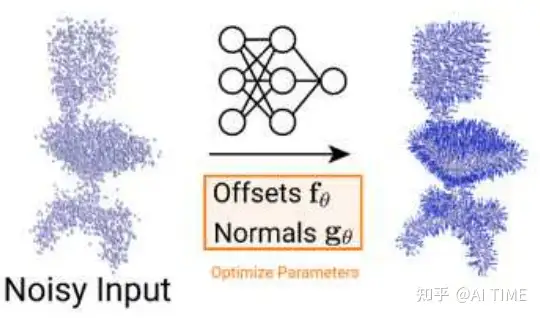
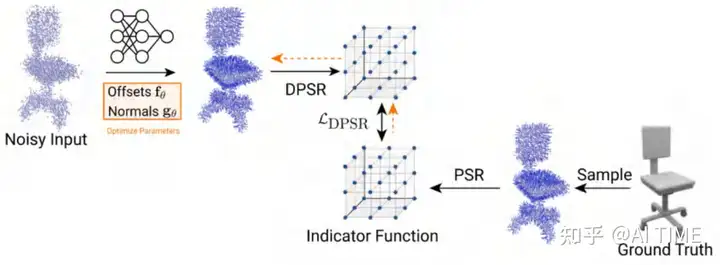
假设我们有一个noisy的输入，目的是学习上图这样的网络，这个网络可以估计当前点云怎样移动以及其法向量是什么样的。

然后我们将上图中的输出输入到DPSR中。

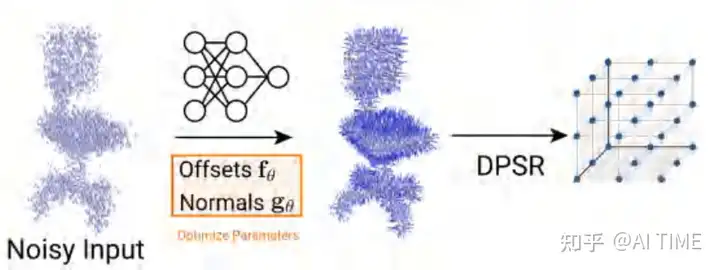
我们从DPSR中获取来Indicator Function指示场。下面是GroundTruth的指示场获取过程。

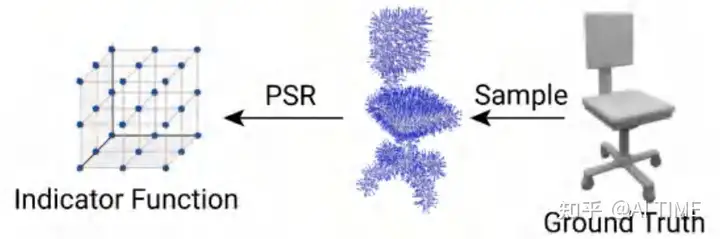
最后，我们就用上述两种方式取得的Indicator Function指示场求得一个loss，并通过DPSR回传求导得到的Gradient来update我们的网络。

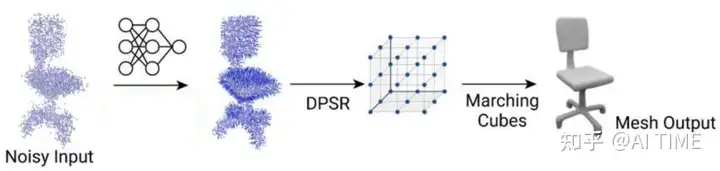
在inference的时候，最后获取march输出过程如下：

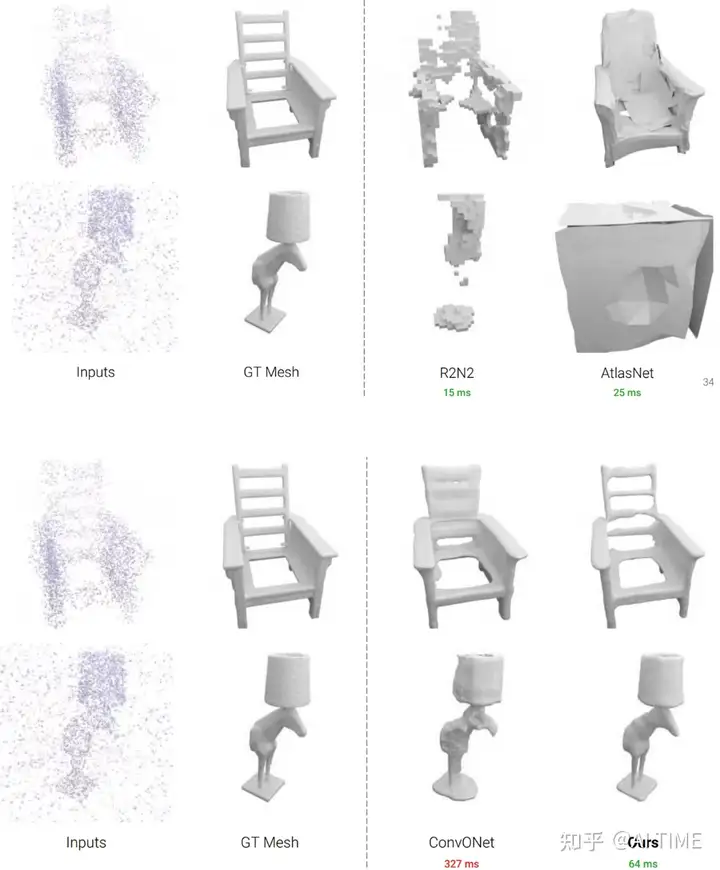
Results

Benefit of Geometric Initialization

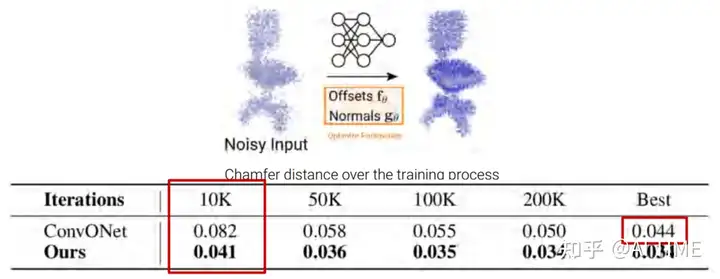
虽然我们可以把输入的点云进行几何的初始化，但我们发现SAP converges是运行最快的。

Conclusions

我们提出了一种泊松求解器SAP：

SAP是可解释的，轻量级和保证HQ watertight meshesSAP也是拓扑无关的，支持快速inference我们的泊松求解器是可微的和GPU加速的

Limitation

内存呈立方提升，所以会被限制在比较小的场景中。

论文题目：

Shape As Points: A Differentiable Poisson Solver

论文链接：

https://proceedings.neurips.cc/paper/2021/hash/6cd9313ed34ef58bad3fdd504355e72c-Abstract.html