数值分析(6)-函数逼近的基本概念

 

1. 函数逼近与函数空间

1.1 常见的一次近似式 (|x|很小时,泰勒多项式)

1.2 函数逼近

对函数类A中给定的f(x)，记作f(x)∈A,要在另一类简单的便于计算的函数类B中求函数p(x)∈B，使f(x)和p(x)误差在某种度量意义下最小。

函数类A通常是区间[a,b]上的连续函数，记作C[a,b]，称为来连续函数空间。函数类B通常为n次多项式，有理函数或分段低次多项式等。

数学上常把各种集合中引入某些不同的确定关系称为赋予集合以某种空间结构，并将这样的集合称为空间。

对次数不超过nnn的实系数多项式全体，按通常多项式与多项式假发及数与多项式乘法构成数域R上的一个线性空间，称为多项式空间。

2. 范数与赋范线性空间

定义2: 设S为线性空间，x∈S若存在唯一实数，||⋅||满足条件：

||x||≥0，当且仅当x=0时∣∣x∣∣=0||x||=0∣∣x∣∣=0（正定性）

||αx||=|α|||x||，α∈R（齐次性）

||x+y||≤||x||+||y||，x,y∈S（三角不等式）

则称||⋅||为线性空间S上得范数，S与||⋅|一起称为赋范线性空间，记为X。

3. 内积和内积空间

定义3：X是数域K上的线性空间，对所有的u，v∈X,K中一个数与之对应，记为(u,v)它满足以下条件：

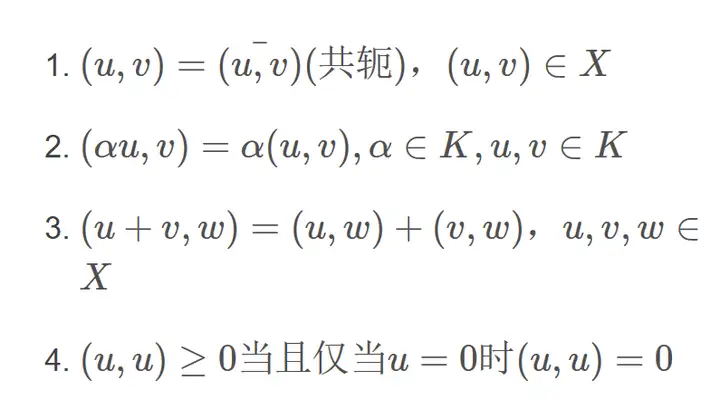
则称(u,v)为X上u与v的内积，内积的线性空间称为内积空间，当K为实数域R时(u,v)=(v,u)，若(u,v)=0则称u与v正交。

4. 逼近的度量标准

{持续更新}

欢迎关注 深度学习与数学 [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读，算法和其他互联网技能的学习，概率论、线性代数等高等数学知识的回顾]