数值分析 - 第二章 - 函数逼近 （1） - 最佳平方逼近

写在前面

上一章我们学习了关于插值的一些知识，接下来讲函数逼近。

插值和函数逼近有很大的相似性，但是插值得到的函数是要过所有已知数据点的，而函数逼近得到的函数与已知的函数/数据点是存在一定误差的。两者没有绝对的优劣，根据实际情况自行选用即可。（需要过已知数据点的，就用插值，不需要的，就用函数逼近。）

闲话少叙，开讲。

背景

有时候我们会计算得到一个非常复杂的函数，比如

f(x)=ex+x5+ln⁡3xx7f(x)=\frac{\sqrt{e^x+x^5}+\ln3x}{x^7}\\

（随便举个例子）

这个东西看起来是挺酷的，但是无论是后续继续做公式推导还是数值计算，都很让人头疼。如果能以损失一些精度为代价来用一些简单函数（比如多项式函数）拟合他的话，那一定是一件很不错的事情。

例如当 xx 取值比较小的时候，可以用 x+1x+1 来拟合 exe^x

定义

最佳平方逼近函数

对于 f(x)∈C[a,b]f(x)\in C[a,b] 及 C[a,b]C[a,b] 中的一个子集 φ=span{φ0(x),φ1(x),⋯,φn(x)}\varphi = {\rm span}\{\varphi_0(x),\varphi_1(x),\cdots,\varphi_n(x)\} 若存在 S∗(x)∈φS^*(x)\in\varphi 使

||f(x)−S∗(x)||22=minS(x)∈φ||f(x)−S(x)||22=minS(x)∈φ∫abρ(x)[f(x)−S(x)]2dx\begin{aligned} ||f(x)-S^*(x)||_2^2&=\min_{S(x)\in\varphi}||f(x)-S(x)||_2^2\\ &=\min_{S(x)\in\varphi}\int_a^b\rho(x)[f(x)-S(x)]^2{\rm d}\,x \end{aligned}\\

则称 S∗(x)S^*(x) 是 f(x)f(x) 在子集 φ⊂C[a,b]\varphi\subset C[a,b] 中的最佳平方逼近函数。

说人话就是，对于给定的一个被逼近函数 f(x)f(x) ，用简单函数 {φ0(x),φ1(x),⋯,φn(x)}\{\varphi_0(x),\varphi_1(x),\cdots,\varphi_n(x)\} 做线性组合来逼近这个函数。

希尔伯特(Hibert)矩阵

H=(11/2⋯1/(n+1)1/21/3⋯1/(n+2)⋮⋮⋮1/(n+1)1/(n+2)⋯1/(2n+1))H=\begin{pmatrix} 1 & 1/2 & \cdots &1/(n+1)\\ 1/2 &1/3 & \cdots & 1/(n+2)\\ \vdots & \vdots & & \vdots \\ 1/(n+1) & 1/(n+2) & \cdots & 1/(2n+1)\end{pmatrix}\\

勒让德(Legendre)多项式

Pn(x)=12nn!dndxn(x2−1)nP_n(x)=\frac{1}{2^nn!}\frac{{\rm d}^n}{{\rm d}x^n}(x^2-1)^n\\

其中

p0(x)=1p1(x)=xp2(x)=32x2−12p3(x)=52x3−32\begin{aligned} p_0(x)&=1\\ p_1(x)&=x\\ p_2(x)&=\frac{3}{2}x^2-\frac{1}{2}\\ p_3(x)&=\frac{5}{2}x^3-\frac{3}{2} \end{aligned}\\

计算方法

方法一

记 di=∫abφi(x)f(x)dxd_i = \int_a^b\varphi_i(x)f(x)\,{\rm d}x ，d=(d0,d1,⋯,dn)T{\bf d}=(d_0,d_1,\cdots,d_n)^T

解方程

Ha=d{\bf Ha}={\bf d}\\

即可得到系数矩阵 a\bf a。（其中H\bf H 是希尔伯特矩阵）。

例一

题目：设 f(x)=1+x2f(x)=\sqrt{1+x^2} ，求 [0,1][0,1] 上的二次最佳平方逼近多项式。

即， φ=span{1,x,x2}\varphi={\rm span}\{1,x,x^2\}

参考答案：

d0=∫011+x2dx=1.1478d1=∫01x1+x2dx=0.6095d1=∫01x21+x2dx=0.4202\begin{aligned} d_0&=\int_0^1\sqrt{1+x^2}{\rm d}x=1.1478\\ d_1&=\int_0^1x\sqrt{1+x^2}{\rm d}x=0.6095\\ d_1&=\int_0^1x^2\sqrt{1+x^2}{\rm d}x=0.4202\\ \end{aligned}

求解方程组

(11/21/31/21/31/41/31/41/5)(a0a1a2)=(1.14780.60950.4202)\begin{pmatrix} 1 & 1/2 &1/3\\ 1/2 & 1/3 & 1/4\\ 1/3 & 1/4 & 1/5 \end{pmatrix} \begin{pmatrix} a_0\\ a_1\\ a_2 \end{pmatrix} = \begin{pmatrix} 1.1478\\ 0.6095\\ 0.4202 \end{pmatrix}\\

得到

a0=0.9938a1=0.0703a2=0.3567\begin{aligned} a_0 &=0.9938\\ a_1 &= 0.0703\\ a_2 &= 0.3567\end{aligned}\\

于是得到

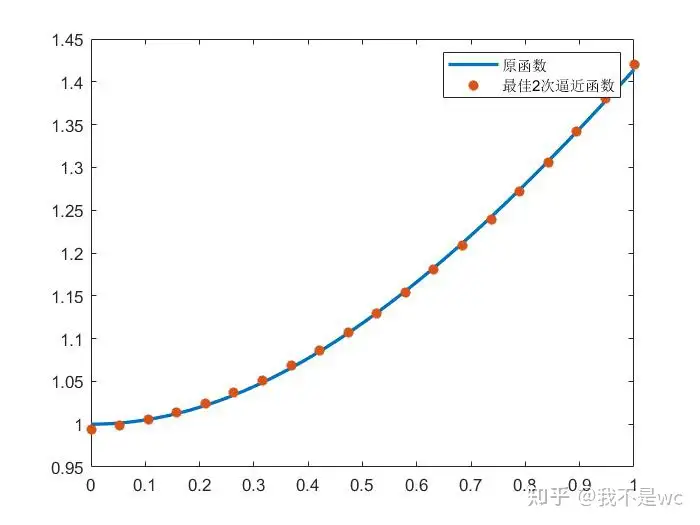
S(x)=0.9938+0.0703x+0.3567x2S(x)=0.9938+0.0703x+0.3567x^2

作图如下

代码如下

如果你真的把跑过我上面的代码，会发现MATLAB会跑出一个跟上面写的不一样的结果，这是由于计算精度导致的（根据我的判断）。我们在上面计算的时候，手动将did_i 保留了四位有效数字，而MATLAB保留的位数更多，原本很小的误差由于希尔伯特矩阵具有高度病态性，将这一误差放大，从而得到了不同的结果。

为了避免这一问题，可以使用下面的方法来计算。（利用了正交多项式—勒让德多项式）

方法二

Sn(x)=a0P0(x)+a1P1(x)+⋯+anPn(x)S_n(x)=a_0P_0(x)+a_1P_1(x)+\cdots+a_nP_n(x)\\

其中， Pi(x)P_i(x) 是勒让德多项式， ai=2i+12∫−11f(x)pi(x)dxa_i=\frac{2i+1}{2}\int_{-1}^{1}f(x)p_i(x){\rm d}\,x ， Sn(x)S_n(x) 即为最后的结果 。

注意：此方法只适用于在 [−1,1]\bf [-1,1]上的最佳平方逼近 多项式。

如果逼近区间不是 [−1,1][-1,1]，那么需要做线性替换将逼近区间变换到[−1,1][-1,1] 上，再将最后的结果变换回原逼近区间。

例二

题目：设 f(x)=exf(x)=e^x ，求 [−1,1][-1,1] 上的二次最佳平方逼近多项式。

参考答案：

a0=12∫−11exdx=1.1752a1=32∫−11xexdx=1.1036a2=52∫−11(32x2−12)exdx=0.3578a3=72∫11(52x3−32x)exdx=0.07046\begin{aligned} a_0&=\frac{1}{2}\int_{-1}^1e^x{\rm d}x=1.1752\\ a_1&=\frac{3}{2}\int_{-1}^1xe^x{\rm d}x=1.1036\\ a_2&=\frac{5}{2}\int_{-1}^1(\frac{3}{2}x^2-\frac{1}{2})e^x{\rm d}x=0.3578\\ a_3&=\frac{7}{2}\int_1^1(\frac{5}{2}x^3-\frac{3}{2}x)e^x{\rm d}x=0.07046 \end{aligned}\\

于是得到

S(x)=a0p0(x)+a1p1(x)+a2p2(x)+a3p3(x)=0.9963+0.9979x+0.8367x2+0.1761x3S(x)=a_0p_0(x)+a_1p_1(x)+a_2p_2(x)+a_3p_3(x)=0.9963+0.9979x+0.8367x^2+0.1761x^3\\

例三

题目：设 f(x)=1+x2f(x)=\sqrt{1+x^2} ，求 [0,1][0,1] 上的二次最佳平方逼近多项式。

参考答案：

令 t=1b−a(2x−a−b)t=\frac{1}{b-a}(2x-a-b) 即 x=1−02t+1+02=12t+12x = \frac{1-0}{2}t+\frac{1+0}{2}=\frac{1}{2}t+\frac{1}{2}

得到 f(x)=g(t)=(t2+12)2+1f(x)=g(t)=\sqrt{\left(\frac{t}{2}+\frac{1}{2}\right)^2+1}

计算得到

a0=12∫−11g(t)dt=1.1478a1=32∫−11tg(t)dt=0.2135a2=52∫−11(32t2−12)g(t)dt=0.0594\begin{aligned} a_0&=\frac{1}{2}\int_{-1}^1g(t){\rm d}t=1.1478\\ a_1&=\frac{3}{2}\int_{-1}^1tg(t){\rm d}t=0.2135\\ a_2&=\frac{5}{2}\int_{-1}^1(\frac{3}{2}t^2-\frac{1}{2})g(t){\rm d}t=0.0594\\ \end{aligned}\\

于是

M(t)=a0P0(t)+a1P1(t)+a2P2(t)=0.0892t2+0.2135t+1.1181M(t)=a_0P_0(t)+a_1P_1(t)+a_2P_2(t)=0.0892t^2+0.2135t+1.1181\\

利用 t=1b−a(2x−a−b)t=\frac{1}{b-a}(2x-a-b) 得到

S(x)=M(t)=0.3567x2+0.0703x+0.9938S(x)=M(t)=0.3567x^2+0.0703x+0.9938\\

可以发现，例三的答案与例一的答案有所不同，这正是因为希尔伯特矩阵高度病态。因此，我们一般采用方法二来计算最佳平方逼近多项式。

代码如下

写在后面

除了文中提到的两种方法，还有利用 切比雪夫多项式 来做函数逼近的，就不在这里细说了。详情可见参考书目

我不是wc：数值分析 | 引言与专栏目录17 赞同 · 4 评论文章