价差组合
除了执行价格K不同其他条件均相同的两个或多个同种期权构造的交易策略,主要介绍牛市价差、熊市价差、蝶式价差策略与盒式价差。
一、牛市价差组合(bull spread)——买低卖高
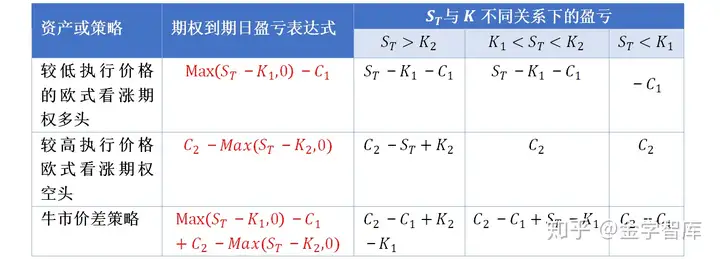
1.看涨期权构造牛市价差组合。该策略持有一个较低执行价格的欧式看涨期权多头头寸,同时持有一个较高执行价格的欧式看涨期权空头头寸,这两个期权的基础资产和合约期限均相同。如果投资者认为未来基础资产价格将保持震荡上行的趋势,就可采用牛市价差策略。
K1:较低期权的执行价格;
K2:较高期权的执行价格;
C1:较低执行价格期权的当前价格;
C2:较高执行价格期权的当前价格;
S0:标的资产当前单位净值价格;
ST:标的资产期权到期日单位净值价格;
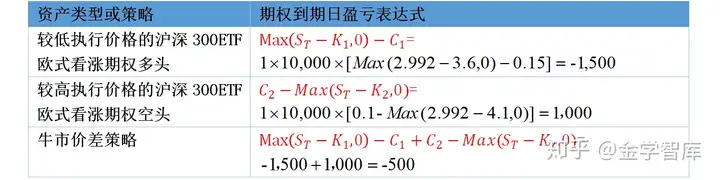
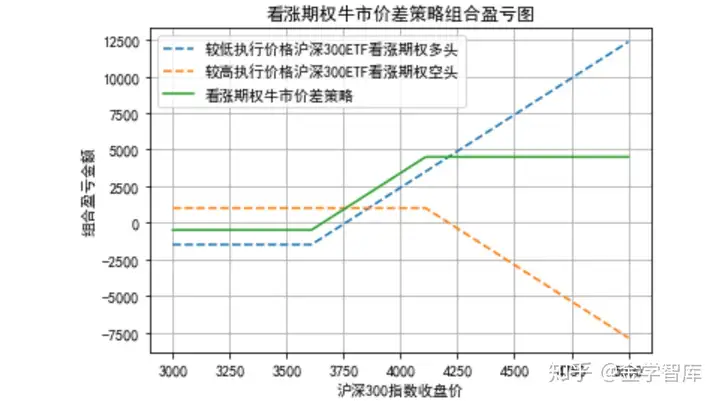
【案例分析1】A机构要运用沪深300ETF期权构建牛市价差策略。一个期权是较低的执行价格K1=3.6元,期权费为C1=0.15元;另一个期权是较高执行价格K2=4.1元,期权费为C2=0.1元,策略构建当天沪深300指数ETF基金的净值是3.8630,沪深300指数点数为3872.7701。A机构运用一张执行价格3.6元的沪深300ETF看涨期权多头头寸和一张执行价格4.1元的沪深300 ETF看涨期权空头头寸构建牛市价差策略(假定到期日指数收盘价的范围在3000~5000)。
【注】一张期权的基础资产是10000份沪深300ETF。
①假定沪深300指数跌至3000点:
单位净值=3000×3.8630/3872.7701=2.992
②假定沪深300指数上升至5000点:
单位净值=5000×3.8630/3872.7701=4.9874
Python实现:
import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams[font.sans-serif]=[SimHei]
mpl.rcParams[axes.unicode_minus]=False
#看涨期权构造牛市价差策略
def bullspread_call(K1,K2,C1,C2,P0,P0_index,Pt_index,N1,N2,N_underlying):
K1:较低期权的执行价格;
K2:较高期权的执行价格;
C1:较低执行价格期权的当前价格;
C2:较高执行价格期权的当前价格;
P0:标的资产当前单位净值价格;
P0_index:标的资产当前收盘点位; Pt_index:期权到期日标的资产收盘点位;
N1:较低执行价格的期权多头头寸数量;
N2:较高执行价格的期权多头头寸数量;
N_underlying:1张标的资产期权基础资产是多少份单位净值.
Pt=P0*Pt_index/P0_index #期权到期日标的资产基金净值数组
call_long=N1*N_underlying*(np.maximum(Pt-K1,0)-C1) #期权到期日较低执行价格期权多头头寸的盈亏
call_short=N2*N_underlying*(C2-np.maximum(Pt-K2,0)) #期权到期日较高执行价格期权空头头寸的盈亏
bull_spread=call_long+call_short
return Pt_index,call_long,call_short,bull_spread #期权到期日牛市价差盈亏
A=bullspread_call(K1=3.6,K2=4.1,C1=0.15,C2=0.1,P0=3.8630,P0_index=3872.7701,Pt_index=np.linspace(3000,5000,500),
N1=1,N2=1,N_underlying=10000)
plt.plot(A[0],A[1],--,label=较低执行价格沪深300ETF看涨期权多头)
plt.plot(A[0],A[2],--,label=较高执行价格沪深300ETF看涨期权空头)
plt.plot(A[0],A[3],label=看涨期权牛市价差策略)
plt.xlabel(沪深300指数收盘价)
plt.ylabel(组合盈亏金额)
plt.title(看涨期权牛市价差策略组合盈亏图)
plt.legend()
plt.grid()
2.看跌期权构造牛市价差组合。用看跌期权构造牛市价差策略可以由较低执行价格的欧式看跌期权多头头寸和较高执行价格的欧式看跌期权的空头头寸构造而成。
K1:较低期权的执行价格;
K2:较高期权的执行价格;
P1:较低执行价格期权的当前价格;
P2:较高执行价格期权的当前价格;
S0:标的资产当前单位净值价格;
ST:标的资产期权到期日单位净值价格;
【案例分析2】B机构要构建牛市价差策略,策略构建的时间是2020年8月27日,2个看跌期权均是在2020年12月23日到期的沪深300ETF期权。其中,一个期权是较低的执行价格为K1=3.6元,期权价格是P1=0.1元;另一个期权是较高执行价格K2=4.1元,期权的价格是P2=0.3元,策略构建当天沪深300ETF基金的净值是3.8630,沪深300指数点数为3872.7701。因此,金融机构运用一张执行价格3.6元的沪深300指数ETF看跌期权多头头寸和一张执行价格4.1元的沪深300ETF看跌期权空头头寸构建牛市价差策略(假定到期日指数收盘价的范围在3000~5000)。
Python实现:
#看跌期权构造牛市价差策略
def bullspread_put(K1,K2,P1,P2,P0,P0_index,Pt_index,N1,N2,N_underlying):
K1:较低期权的执行价格;
K2:较高期权的执行价格; P1:较低执行价格期权的当前价格;
P2:较高执行价格期权的当前价格;
P0:标的资产当前单位净值价格;
P0_index:标的资产当前收盘点位;
Pt_index:期权到期日标的资产收盘点位; N1:较低执行价格的期权多头头寸数量;
N2:较高执行价格的期权多头头寸数量;
N_underlying:1张标的资产期权基础资产是多少份单位净值.
Pt=P0*Pt_index/P0_index #期权到期日标的资产基金净值数组
put_long=N1*N_underlying*(np.maximum(K1-Pt,0)-P1) #期权到期日较低执行价格期权多头头寸的盈亏
put_short=N2*N_underlying*(P2-np.maximum(K2-Pt,0)) #期权到期日较高执行价格期权空头头寸的盈亏
bull_spread=put_long+put_short
return Pt_index,put_long,put_short,bull_spread #期权到期日牛市价差盈亏
B=bullspread_put(K1=3.6,K2=4.1,P1=0.1,P2=0.3,P0=3.8630,P0_index=3872.7701,Pt_index=np.linspace(3000,5000,500),
N1=1,N2=1,N_underlying=10000)
plt.plot(B[0],B[1],--,label=较低执行价格沪深300ETF看跌期权多头)
plt.plot(B[0],B[2],--,label=较高执行价格沪深300ETF看跌期权空头)
plt.plot(B[0],B[3],label=看跌期权牛市价差策略)
plt.xlabel(沪深300指数收盘价)
plt.ylabel(组合盈亏金额)
plt.title(看跌期权牛市价差策略组合盈亏图)
plt.legend()
plt.grid()
二、熊市价差策略(bear spread)——买高卖低
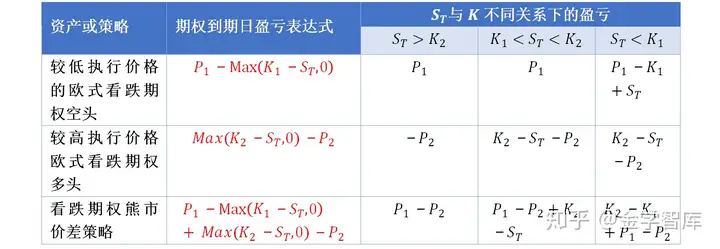
1.看跌期权构造熊市价差组合。该策略持有一个较高执行价格的欧式看跌期权多头头寸和一个较低执行价格的欧式看跌期权空头头寸,基础资产和合约期限均相同。如果投资者认为未来基础资产价格将下跌,就可采用熊市价差策略。
【案例分析3】C金融机构要构建熊市价差策略,策略构建的时间是2020年8月27日,2个看跌期权均是在2020年12月23日到期的沪深300ETF期权。其中,一个期权是较低的执行价格为K1=3.6元,期权价格是P1=0.08元;另一个期权是较高执行价格K2=4.1元,期权的价格是P2=0.25元,策略构建当天沪深300 ETF基金的净值是3.8630,沪深300指数点数为3872.7701。因此,金融机构运用一张执行价格3.6元的沪深300 ETF看跌期权空头头寸和一张执行价格4.1元的沪深300 ETF看跌期权多头头寸构建牛市价差策略(假定到期日指数收盘价的范围在3000~5000)。
Python实现:
#看跌期权构造熊市价差策略
def bearspread_put(K1,K2,P1,P2,P0,P0_index,Pt_index,N1,N2,N_underlying):
K1:较低期权的执行价格;
K2:较高期权的执行价格;
P1:较低执行价格期权的当前价格;
P2:较高执行价格期权的当前价格;
P0:标的资产当前单位净值价格; P0_index:标的资产当前收盘点位;
Pt_index:期权到期日标的资产收盘点位;
N1:较低执行价格的期权多头头寸数量;
N2:较高执行价格的期权多头头寸数量;
N_underlying:1张标的资产期权基础资产是多少份单位净值.
Pt=P0*Pt_index/P0_index #期权到期日标的资产基金净值数组
put_short=N1*N_underlying*(P1-np.maximum(K1-Pt,0)) #期权到期日较低执行价格期权空头头寸的盈亏
put_long=N2*N_underlying*(np.maximum(K2-Pt,0)-P2) #期权到期日较高执行价格期权多头头寸的盈亏
bear_spread=put_short+put_long
return Pt_index,put_short,put_long,bear_spread #期权到期日熊市价差收益
C=bearspread_put(K1=3.6,K2=4.1,P1=0.08,P2=0.25,P0=3.8630,P0_index=3872.7701,Pt_index=np.linspace(3000,5000,500),
N1=1,N2=1,N_underlying=10000)
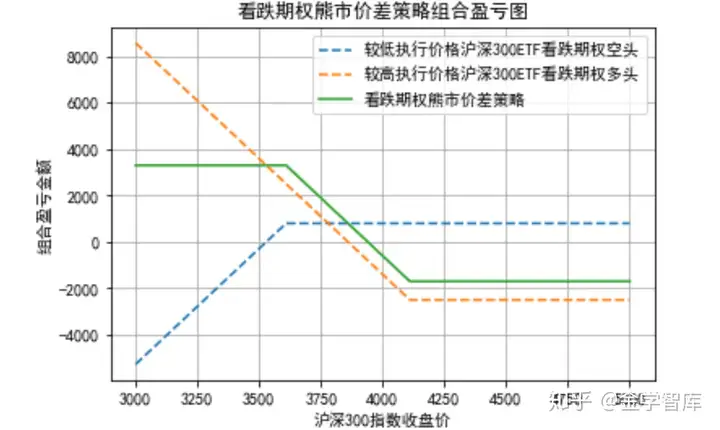
plt.plot(C[0],C[1],--,label=较低执行价格沪深300ETF看跌期权空头)
plt.plot(C[0],C[2],--,label=较高执行价格沪深300ETF看跌期权多头)
plt.plot(C[0],C[3],label=看跌期权熊市价差策略)
plt.xlabel(沪深300指数收盘价)
plt.ylabel(组合盈亏金额)
plt.title(看跌期权熊市价差策略组合盈亏图)
plt.legend()
plt.grid()
2.看涨期权构造熊市价差组合。投资者持有1个较高执行价格的看涨期权多头,同时持有一个较低执行价格的看涨期权空头。
【案例分析4】D金融机构要构建熊市价差策略,策略构建的时间是2020年8月27日,2个看涨期权均是在2020年12月23日到期的沪深300ETF期权。其中,一个期权是较低的执行价格为K1=3.6元,期权价格是C1=0.3元;另一个期权是较高执行价格K2=4.1元,期权的价格是C2=0.1元,策略构建当天沪深300ETF基金的净值是3.8630,沪深300指数点数为3872.7701。因此,金融机构运用一张执行价格3.6元的沪深300ETF看涨期权空头头寸和一张执行价格4.1元的沪深300指数ETF看涨期权多头头寸构建牛市价差策略(假定到期日指数收盘价的范围在3000~5000)。
Python实现:
#看涨期权构造熊市价差策略
def bearspread_call(K1,K2,C1,C2,P0,P0_index,Pt_index,N1,N2,N_underlying):
K1:较低期权的执行价格; K2:较高期权的执行价格;
C1:较低执行价格期权的当前价格;
C2:较高执行价格期权的当前价格;
P0:标的资产当前单位净值价格;
P0_index:标的资产当前收盘点位;
Pt_index:期权到期日标的资产收盘点位; N1:较低执行价格的期权多头头寸数量;
N2:较高执行价格的期权多头头寸数量;
N_underlying:1张标的资产期权基础资产是多少份单位净值.
Pt=P0*Pt_index/P0_index #期权到期日标的资产基金净值数组
call_short=N1*N_underlying*(C1-np.maximum(Pt-K1,0)) #期权到期日较低执行价格期权空头头寸的盈亏
call_long=N2*N_underlying*(np.maximum(Pt-K2,0)-C2) #期权到期日较高执行价格期权多头头寸的盈亏
bear_spread=call_short+call_long
return Pt_index,call_short,call_long,bear_spread #期权到期日熊市价差盈亏
D=bearspread_call(K1=3.6,K2=4.1,C1=0.3,C2=0.1,P0=3.8630,P0_index=3872.7701,Pt_index=np.linspace(3000,5000,500),
N1=1,N2=1,N_underlying=10000)
plt.plot(D[0],D[1],--,label=较低执行价格沪深300ETF看涨期权空头)
plt.plot(D[0],D[2],--,label=较高执行价格沪深300ETF看涨期权多头)
plt.plot(D[0],D[3],label=看跌期权熊市价差策略)
plt.xlabel(沪深300指数收盘价)
plt.ylabel(组合盈亏金额)
plt.title(看涨期权熊市价差策略组合盈亏图)
plt.legend()
plt.grid()
三、蝶式价差策略(butterfly spread)
1.采用看涨期权构造蝶式价差策略。看涨期权蝶式价差由3种K不同而其他条件相同的期权构成,构造方式是一个较低执行价格K1的欧式看涨期权多头 + 一个较高执行价格K3的欧式看涨期权多头头寸 + 两个执行价格K2的欧式看涨期权空头头寸,其中即K2=(K1+K3)/2。一般来讲K2接近于当前基础资产价格。蝶式价差策略对于那些认为基础资产价格不会有太大波动的投资者而言会比较合适,因为该策略仅仅需要较少的期初投资成本。
【注】当ST>K3或ST<K3时,该策略的损益均为固定值。
【案例分析5】F金融机构要构建蝶式价差策略,策略构建的时间是2020年8月27日,运用的4个期权均是在2020年12月23日到期的沪深300指数ETF期权,具体的信息如下:
较低期的期权执行价格K1=3.6
中间的期权执行价格K2=4.1
较高的期权执行价格K3=4.6
较低执行价格看涨期权的当前价格C1=0.3
中间价格看涨期权的当前价格C2=0.1
较高执行价格看涨期权的当前价格C3=0.05
沪深300指数ETF基金当前价格P0=3.8630
沪深300指数P0_index=3872.7701
期权到期日沪深300指数的收盘价范围Pt_index=[3000, 5000]
较低价格看涨期权头寸数量N1=1
中间价格看涨期权头寸数量N2=2
较高价格看涨期权头寸数量N3=1
1张期权对应的沪深300指数基金份数N_underlying=10000
该金融机构采用1张执行价格为K1=3.6元的看涨期权多头头寸、1张执行价格为K3=4.6元的看涨期权多头头寸、以及2张执行价格为K2=4.1元的看涨期权空头头寸来构建盒式价差策略。
Python实现:
#蝶式看涨期权价差策略
def butterflyspread_call(K1,K2,K3,C1,C2,C3,P0,P0_index,Pt_index,N1,N2,N3,N_underlying):
K1:较低期权的执行价格;
K2:中间的期权执行价格;
K3:较低期的期权执行价格;
C1:较低执行价格看涨期权的当前价格;
C2:中间价格看涨期权的当前价格; C3:较高执行价格看涨期权的当前价格
P0:标的资产当前单位净值价格;
P0_index:标的资产当前收盘点位;
Pt_index:期权到期日标的资产收盘点位;
N1:较低价格看涨期权头寸数量; N2:中间价格看跌期权头寸数量;
N3:较高价格看涨期权头寸数量;
N_underlying:1张标的资产期权基础资产是多少份单位净值.
Pt=P0*Pt_index/P0_index #期权到期日标的资产基金净值数组
call_long1=N1*N_underlying*(np.maximum(Pt-K1,0)-C1) #期权到期日较低执行价格看涨期权多头头寸的盈亏
call_short=N2*N_underlying*(C2-np.maximum(Pt-K2,0)) #期权到期日中间执行价格看涨期权空头头寸的盈亏
call_long2=N1*N_underlying*(np.maximum(Pt-K3,0)-C3) #期权到期日较高执行价格看涨期权多头头寸的盈亏
butterfly_spread=call_long1+call_short+call_long2 #期权到期日蝶式看涨期权价差策略盈亏
return Pt_index,call_long1,call_short,call_long2,butterfly_spread #返回各个策略盈亏
F=butterflyspread_call(K1=3.6,K2=4.1,K3=4.6,C1=0.3,C2=0.1,C3=0.05,
P0=3.8630,P0_index=3872.7701,Pt_index=np.linspace(3000,5000,500),
N1=1,N2=2,N3=1,N_underlying=10000)
plt.plot(F[0],F[1],b--,label=较低执行价格沪深300ETF看涨期权多头)
plt.plot(F[0],F[2],g--,label=中间执行价格沪深300ETF看涨期权空头)
plt.plot(F[0],F[3],r--,label=较高执行价格沪深300ETF看涨期权多头)
plt.plot(F[0],F[4],label=蝶式看涨期权价差策略)
plt.xlabel(沪深300指数收盘价)
plt.ylabel(组合盈亏金额)
plt.title(蝶式看涨期权价差策略组合盈亏图)
plt.legend()
plt.grid()

2.采用看跌期权构造蝶式价差策略。具体如下:一个较低执行价格K1与一个具有较高执行价格K3的欧式看跌期权多头头寸,两个具有中间执行价格K2的欧式看跌期权空头头寸。
【案例分析6】G金融机构要构建蝶式价差策略,策略构建的时间是2020年8月27日,运用的4个期权均是在2020年12月23日到期的沪深300指数ETF期权,具体的信息如下:
较低期的期权执行价格K1=3.6
中间的期权执行价格K2=4.1
较高的期权执行价格K3=4.6
较低执行价格看跌期权的当前价格P1=0.2
中间价格看跌期权的当前价格P2=0.15
较高执行价格看跌期权的当前价格P3=0.1
沪深300指数ETF基金当前价格P0=3.8630
沪深300指数P0_index=3872.7701
期权到期日沪深300指数的收盘价范围Pt_index=[3000,5000]
较低价格看跌期权头寸数量N1=1
中间价格看跌期权头寸数量N2=2
较高价格看跌期权头寸数量N3=1
1张期权对应的沪深300指数基金份数N_underlying=10000
该金融机构采用1张执行价格为K1=3.6元的看跌期权多头头寸、1张执行价格为K3=4.6元的看跌期权多头头寸、以及2张执行价格为K2=4.1元的看跌期权空头头寸来构建盒式价差策略。
Python实现:
#蝶式看跌期权价差策略
def butterflyspread_put(K1,K2,K3,P1,P2,P3,P0,P0_index,Pt_index,N1,N2,N3,N_underlying):
K1:较低期权的执行价格;
K2:中间的期权执行价格;
K3:较低期的期权执行价格;
P1:较低执行价格看涨期权的当前价格; P2:中间价格看涨期权的当前价格;
P3:较高执行价格看涨期权的当前价格
P0:标的资产当前单位净值价格;
P0_index:标的资产当前收盘点位;
Pt_index:期权到期日标的资产收盘点位; N1:较低价格看涨期权头寸数量;
N2:中间价格看跌期权头寸数量;
N3:较高价格看涨期权头寸数量;
N_underlying:1张标的资产期权基础资产是多少份单位净值.
Pt=P0*Pt_index/P0_index #期权到期日标的资产基金净值数组
put_long1=N1*N_underlying*(np.maximum(K1-Pt,0)-P1) #期权到期日较低执行价格看涨期权多头头寸的盈亏
put_short=N2*N_underlying*(P2-np.maximum(K2-Pt,0)) #期权到期日中间执行价格看涨期权空头头寸的盈亏
put_long2=N1*N_underlying*(np.maximum(K3-Pt,0)-P3) #期权到期日较高执行价格看涨期权多头头寸的盈亏
butterfly_spread=put_long1+put_short+put_long2 #期权到期日蝶式看涨期权价差策略收益
return Pt_index,put_long1,put_short,put_long2,butterfly_spread #返回各个策略收益
G=butterflyspread_put(K1=3.6,K2=4.1,K3=4.6,P1=0.2,P2=0.15,P3=0.1,
P0=3.8630,P0_index=3872.7701,Pt_index=np.linspace(3000,5000,500),
N1=1,N2=2,N3=1,N_underlying=10000)
plt.plot(G[0],G[1],b--,label=较低执行价格沪深300ETF看跌期权多头)
plt.plot(G[0],G[2],g--,label=中间执行价格沪深300ETF看跌期权空头)
plt.plot(G[0],G[3],r--,label=较高执行价格沪深300ETF看跌期权多头)
plt.plot(G[0],G[4],label=蝶式看跌期权价差策略)
plt.xlabel(沪深300指数收盘价)
plt.ylabel(组合盈亏金额)
plt.title(蝶式看跌期权价差策略组合盈亏图)
plt.legend()
plt.grid()

【注】盒式价差策略的盈亏为固定值。
四、盒式价差策略(box spread)
盒式价差策略也称为箱式价差策略,是由执行价格为K1与K2的欧式看涨期权所构成的牛市价差策略与具有相同执行价格欧式看跌期权所构成的熊市价差策略的一个组合。其中,K1<K2.
【注】盒式价差策略的盈亏为固定值。
【案例分析7】E金融机构要构建盒式价差策略,策略构建的时间是2020年8月27日,运用的4个期权均是在2020年12月23日到期的沪深300指数ETF期权,具体的信息如下:
较低期的期权执行价格K1=3.6
较高的期权执行价格K2=4.2
较低执行价格看涨期权的当前价格C1=0.2
较高执行价格看涨期权的当前价格C2=0.05
较低执行价格看跌期权的当前价格P1=0.2
较高执行价格看跌期权的当前价格P2=0.3
沪深300指数ETF基金当前价格P0=3.8630
沪深300指数P0_index=3872.7701
期权到期日沪深300指数的收盘价范围Pt_index=[3000,5000]
看涨期权头寸数量N_call=1
看跌期权头寸数量N_put=1
1张期权对应的沪深300指数基金份数N_underlying=10000
该金融机构采用1张执行价格为K1=3.6元的看涨期权多头头寸、1张执行价格为K2=4.2元的看涨期权空头头寸、1张执行价格为K1=3.6元的看跌期权空头头寸、1张执行价格为K2=4.2元的看跌期权多头头寸来构建盒式价差策略。
Python实现:
#盒式价差策略
def boxspread(K1,K2,C1,C2,P1,P2,P0,P0_index,Pt_index,N_call,N_put,N_underlying):
K1:较低期权的执行价格;
K2:较高期权的执行价格;
C1:较低执行价格看涨期权的当前价格;
C2:较高执行价格看涨期权的当前价格;
P1:较低执行价格看跌期权的当前价格 P2:较高执行价格看跌期权的当前价格
P0:标的资产当前单位净值价格;
P0_index:标的资产当前收盘点位;
Pt_index:期权到期日标的资产收盘点位;
N_call:看涨期权头寸数量;
N_put:看跌期权头寸数量; N_underlying:1张标的资产期权基础资产是多少份单位净值.
Pt=P0*Pt_index/P0_index #期权到期日标的资产基金净值数组
call_long=N_call*N_underlying*(np.maximum(Pt-K1,0)-C1) #期权到期日较低执行价格看涨期权多头头寸的盈亏
call_short=N_call*N_underlying*(C2-np.maximum(Pt-K2,0)) #期权到期日较高执行价格看涨期权空头头寸的盈亏
put_short=N_put*N_underlying*(P1-np.maximum(K1-Pt,0)) #期权到期日较低执行价格看跌期权空头头寸的盈亏
put_long=N_put*N_underlying*(np.maximum(K2-Pt,0)-P2) #期权到期日较高执行价格看跌期权多头头寸的盈亏
box_spread=call_long+call_short+put_short+put_long #期权到期日盒式价差策略盈亏
return Pt_index,call_long,call_short,put_short,put_long,box_spread #返回各个策略盈亏
E=boxspread(K1=3.6,K2=4.2,C1=0.2,C2=0.05,P1=0.2,P2=0.3,
P0=3.8630,P0_index=3872.7701,Pt_index=np.linspace(3000,5000,500),
N_call=1,N_put=1,N_underlying=10000)
plt.plot(E[0],E[1],b--,label=较低执行价格沪深300ETF看涨期权多头)
plt.plot(E[0],E[2],g--,label=较高执行价格沪深300ETF看涨期权空头)
plt.plot(E[0],E[3],c--,label=较低执行价格沪深300ETF看跌期权空头)
plt.plot(E[0],E[4],m--,label=较高执行价格沪深300ETF看跌期权多头)
plt.plot(E[0],E[5],label=盒式价差策略)
plt.xlabel(沪深300指数收盘价)
plt.ylabel(组合盈亏金额)
plt.title(盒式价差策略组合盈亏图)
plt.legend()
plt.grid()

从上图计算的损益结果可以看出,在期权到期日无论基础资产如何变化,盒式价差策略的盈亏总是不变的。
附录:欢迎大家关注微信公众号了解更多!谢谢