视觉目标检测与跟踪-经典视觉目标跟踪方法

 

被跟踪对象可以用它们的形状和表观来表示。

常用的对象形状表示方法：点、基本几何形状、轮廓和廓影、关节形状模型、骨架模型。

常用的表观表示方法：

1）概率密度

对象表观的概率密度可以是参数的，也可以是非参数的。参数的表示包括高斯和混合高斯两种类型，非参数的表示包括核密度估计和直方图。对象表观特征（颜色、纹理等）的概率密度可以从形状模型（椭圆、轮廓等）指定的图像区域计算得到。

2）模板

模板通常有简单的几何形状（如矩形等）或廓影组成。

3）主动表观模型

4）多视表观模型

总结：被跟踪对象的表示方法往往和采用的跟踪算法紧密相关，并与具体应用领域相关。如果被跟踪对象在图像中占有区域很小，那么采用点表示是合适的。如果被跟踪对象的形状能够很好的由矩形或椭圆近似，那采用基本几何形状是可行的。如果被跟踪对象具有复杂的形状，那采用轮廓及廓影来表示被跟踪对象是恰当的。

经典视觉目标跟踪方法

确定性目标跟踪方法

确定性视觉目标跟踪方法根据跟踪目标的表示方法和相似性度量方法的不同可以分为：基于特征匹配的跟踪方法、基于区域统计匹配的跟踪方法、基于模型匹配的跟踪方法和基于Mean−ShiftMean-Shift 的跟踪方法。

（1）基于特征匹配的跟踪方法不考虑运动的整体特征，而是通过其特征（如SIFT特征点等）来进行跟踪。主要包括特征提取和特征匹配两个过程。在后续的视频帧中提取相应的特征并于特征模板进行匹配。

（2）基于区域统计匹配的跟踪方法将运动目标连通区域的共有特征信息（颜色特征、纹理特征等）作为追踪特征的一种方法。通过计算候选区域与原始目标之间的区域统计特征的相关性来确定跟踪目标的最佳位置。而不需要在视频序列中找到完全相同的特征信息。

（3）基于模板匹配的跟踪方法是通过建立模型来表示目标，即对运动目标进行建模，然后在图像序列中匹配这个建立好的模型来实现目标的跟踪。

（4）基于 Mean−ShiftMean-Shift的目标跟踪方法采用加权的灰度或颜色直方图来描述跟踪的目标，并通过梯度下降的方式快速迭代的查找跟踪目标。

补充概念：跟踪目标相似度度量

方法有欧氏距离、街区距离、棋盘距离、加权距离、巴特查理亚系数、Hausdorff距离等。其中，Hausdorff距离常用于衡量特征集之间的相似性；直方图之间的相似性采用巴特查理亚系数。

1）欧氏距离

两个点 P1,P2P_1,P_2 坐标分别为 P1(x,y),P2(x,y)P_1(x,y),P_2(x,y) ，则 P1,P2P_1,P_2 的欧氏距离为坐标向量的平方差之和的平方，用公式表示为

d(P1,P2)=(x1−x2)2+(y1−y2)2d(P_1,P_2)=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}

2）加权距离

两个点 P1,P2P_1,P_2 坐标分别为 P1(x,y),P2(x,y)P_1(x,y),P_2(x,y) ，则 P1,P2P_1,P_2的加权距离为坐标向量的每一项的绝对距离的加权和，用公式表示为：

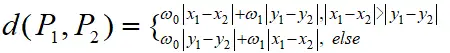
式中， ωi\omega_i 为权重，且 ，ωi≻0，i=1,2\omega_i\succ0，i=1,2

街区距离、棋盘距离是加权距离特殊情况： 当，ω0=1，ω1=1\omega_0=1，\omega_1=1 时，为街区距离，即坐标向量每一项的绝对距离之和；当 ，ω0=1，ω1=0\omega_0=1，\omega_1=0时，加权距离就是棋盘距离，即坐标向量第一项的绝对距离之和。

3）巴特查理亚系数

两个点 P1,P2P_1,P_2 坐标分别为 P1(x1,x2,...,xm),P2(x1,x2,...,xm)P_1(x_1,x_2,...,x_m),P_2(x_1,x_2,...,x_m) ，则 P1,P2P_1,P_2 的巴特查理亚系数为坐标向量的每一项的乘积的开方，用公式表示为：

d(P1,P2)=∑i=1mxiyid(P_1,P_2)=\sum_{i=1}^{m}{\sqrt{x_iy_i}}

4)Hausdorff距离

度量的是两个特征点集之间的相似度。假设有两组有限像素点集合 A={a1,a2,...,ap}A=\left\{ a_1,a_2,...,a_p \right\} 和 B={b1,b2,...,bp}B=\left\{ b_1,b_2,...,b_p \right\} ，则两个点集合之间的HD距离定义为

D(A,B)=max{d(A,B),d(B,A)}D(A,B)=max\left\{d(A,B),d(B,A) \right\}

式中， d(A,B)=maxa∈Aminb∈B||a−b||d(A,B)=\max_{a \in A} \min_{b \in B}{\left|\left| a-b \right| \right|} , d(B,A)=maxb∈Bmina∈A||b−a||d(B,A)=\max_{b \in B} \min_{a \in A}{\left|\left| b-a \right| \right|}。 ||⋅||\left| \left| \cdot \right| \right| 是A和B点集间的某种距离范式。

5）改进的Hausdorff距离

是对HD的改进算法。如基于平均距离值的马氏直方图（MHD）是指先求出点集A中所有点到点集B的距离，然后选择这些距离的平均值，用公式表示为：

dMHD(A,B)=1NA∑ai∈AdB(ai)d_{MHD}(A,B)=\frac{1}{N_A}\sum_{a_i\in A}^{}{d_B(a_i)}

式中， NAN_A 表示集合A中的像素的个数， dB(ai)=minb∈B||ai−b||{d_B(a_i)}=\min_{b \in B}{\left|\left| a_i-b \right| \right|} 表示A集合中的点 aia_i 到集合B的距离，是点 aia_i到集合B中每一点距离的最小值。

基于 Mean−ShiftMean-Shift 的目标跟踪方法

基本 Mean−ShiftMean-Shift

给定d维空间 RdR^d 中的n个样本点 xi,i=1,...,nx_i,i=1,...,n ,则在x点的 Mean−ShiftMean-Shift 向量的基本形式定义为

Mh(x)=1k∑xi∈Sk(xi−x)M_h(x)=\frac{1}{k}\sum_{x_i\in S_k }^{}({x_i-x})

式中，k表示n个样本点落入区域ShS_h中的样本点的个数，ShS_h是一个半径为h的高维球形区域。

Mh(x)M_h(x) 就是对落入区域ShS_h中的k个样本点相对于点x的偏移向量求和，然后平均。指向概率密度梯度的方向。如图

Mean-Shift示意图

非确定性目标跟踪方法

随机性目标跟踪常用的预测算法有卡尔曼滤波以及粒子滤波算法等。利用滤波器来估计目标运动，当系统对目标的运动位置和速度有了可靠估计后，可以在相对较小的区域内进行搜素，完成对目标的跟踪过程。滤波方法的优点：采用递归滤波的方法，可将任意一点作为初始状态开始递归；计算量小；预测具有无偏、稳定、最优等优点。

1.基于卡尔曼滤波器的视觉目标跟踪

卡尔曼滤波是一种对动态系统的状态序列求线性最小均方差估计的算法，利用动态的状态方程和观测方程来描述系统。

2.基于粒子滤波器的视觉目标跟踪

粒子滤波使用了大量随机样本，采用蒙特卡罗仿真来完成递推贝叶斯滤波过程，其核心是使用一组具有相应权值的随机样本（粒子）来表示状态的后验分布。基本思路是选取一个重要性概率密度并从中进行随机抽样，得到一些带有相应权值的随机样本后，在状态观测的基础上调节权值的大小和粒子的位置，再使用这些样本来逼近状态后验分布，最后通过这组样本的加权求和作为状态的估计值。

参考资料