黎巴嫩港口大爆炸到底有多厉害？

 

引言

2020 年 8 月 4 日傍晚，黎巴嫩首都贝鲁特港口区发生剧烈爆炸 [1]，巨响震天升起蘑菇云。爆炸释放了巨大的能量，造成数千人伤亡，数十万人无家可归。爆炸发生瞬间一度被认为是地震、核打击。贝鲁特市长更是把爆炸比作 1945 年日本广岛爆炸的原子弹。

黎巴嫩总理证实爆炸是 6 年前被扣押并存放在港口的 2750 吨硝酸铵引发的。硝酸铵（NH4NO3\mathrm{NH_4NO_3}）是一种铵盐，因含氮量高，被常用于制造高氮化肥。硝酸铵遇热会分解，在不同温度下，硝酸铵会发生不同的化学反应。并且温度越高，反应越迅速。在 110∘C^\circ\mathrm{C} 时：

NH4NO3→NH3+HNO3\mathrm{NH_4NO_3\rightarrow NH_3+HNO_3} \\

在 185-200 ∘C^\circ\mathrm{C} 时：

NH4NO3→N2O+2H2O\mathrm{NH_4NO_3\rightarrow N_2O+2H_2O} \\

在 230 ∘C^\circ\mathrm{C} 以上，伴有弱光：

2NH4NO3→2N2+O2+4H2O\mathrm{2NH_4NO_3\rightarrow 2N_2+O_2+4H_2O} \\

在 400 ∘C^\circ\mathrm{C} 以上，发生爆炸：

4NH4NO3→3N2+2NO2+8H2O\mathrm{4NH_4NO_3\rightarrow 3N_2+2NO_2+8H_2O} \\

从以上反应方程式可以看出，硝酸铵分解会产生大量的气体。一千克硝酸铵爆炸会产生 900 升气体，这些气体会在短时间内释放，产生巨大的压力和气浪，对周围的建筑物造成破坏。因此，硝酸铵也常被作为采矿、采石和土木建筑中使用的爆炸混合物成分之一。纯硝酸铵在常温下是稳定的，对打击、碰撞或摩擦均不敏感。但如果储存时间过长，并且通风不佳，其自身会发生反应产生热量，进而导致温度升高并且燃烧，引发爆炸。

引发贝鲁特港口爆炸事故的原因正在调查，不过也可以估个大概。若非人为，则是由于硝酸铵发生热分解，存料下层集聚的热量未能及时导出，发生自燃并引起爆炸。港口环境复杂，附近很可能还存放有其它易爆物。加之近期贝鲁特气温高达 30 多度，更加为爆炸提供了有利条件。

本次爆炸究竟产生了多大的能量？通常我们用释放相同能量的 TNT 炸药的质量表示爆炸产生的能量，写成 TNT 当量。一吨 TNT 完全爆炸释放的能量等于 4.184×1094.184\times 10^9 J。而一吨硝酸铵完全爆炸释放的能量等于 0.42 吨 TNT，因此贝鲁特港口爆炸当量的理论上限是 0.42×2750=11500.42\times 2750 = 1150吨。如果硝酸铵的有效爆炸率为 25%，则 2750 吨硝酸铵爆炸能量相当于 288 吨 TNT。288 吨 TNT 是什么概念？可以参考一下原子弹的当量，1945 年 8 月 9 日美国在日本长崎投掷的原子弹的 TNT 当量为 1.3 万吨。但本次事故中，我们并不清楚硝酸铵的有效爆炸率到底是多少。

历史最有名的爆炸当量估计是对原子弹爆炸的估计。1945 年 7 月 16 日美国科学家在新墨西哥州阿拉莫戈多沙漠进行了三位一体核试验（Trinity），但是试爆后原子弹的某些属性却并不明朗 [2]。

负责研制核装置的项目组顾问杰弗里·泰勒是一名剑桥大学教授，他亲眼目睹了这场核实验，但是仅靠肉眼并不能估测出原子弹的威力。1947 年之后，三位一体核试验原子弹爆炸的照片逐渐被媒体公开，泰勒根据爆炸后的一系列照片建立数学模型，成功估算出原子弹爆炸时所释放的能量。本文就来展示一下泰勒估计原子弹当量的模型 [3]，并应用该模型对本次贝鲁特港口大爆炸进行分析。

模型

假设点源爆炸球形冲击波的半径（RR）仅仅依赖于爆炸后的时间（tt）、爆炸瞬间所释放的能量（EE）和空气的密度（ρ\rho）。即

R=CtxEyρzR = \textrm{C} ~ t^xE^y\rho^z \\

其中 CC 是无量纲的常数。利用量纲齐次原则（即等式两边的量纲要相同），可以求出 xx、yy、zz 的值。我们将变量替换为各自的基本量纲，例如将半径 RR换成它的量纲 [RR]，本文所涉及到的基本量纲包括质量（M\mathrm{M}），长度（L\mathrm{L}）和时间（T\mathrm{T}），因此变量对应的基本量纲为：[R]=L[R] = \mathrm{L}，[t]=T[t] = \mathrm{T}，[E]=ML2T−2[E] =\mathrm{ML^2T^{-2}}，[ρ]=ML−3[\rho] = \mathrm{ML^{-3}}。将变量各自的量纲代入上式，整理后可得到：

L1=M(y+z)L(2y−3z)T(x−2y)\textrm{L}^1 = \textrm{M}^{(y+z)}\textrm{L}^{(2y-3z)}\textrm{T}^{(x-2y)} \\

由于等式两边的量纲相同，因此

1y+1z=02y−3z=11x−2y=0\begin{aligned} 1y + 1z&= 0\\ 2y − 3z& = 1\\ 1x − 2y& = 0 \end{aligned} \\

联立以上三式即可得到 x=2/5x = 2/5，y=1/5y = 1/5，z=−1/5z = -1/5，所以

R=C(Et2/ρ)1/5R = \textrm{C}(Et^2/\rho)^{1/5} \\

其中 CC 是一个无量纲的常数，是热容比（γ=Cρ/Cv\gamma=C_\rho/C_v，或者称作绝热指数）的低阶函数，因此在任何条件下都近似为 1 [3]。可以推出爆炸所释放的能量

E=ρR5/t2E = \rho R^5/t^2 \\

对上式两端同时除以 ρ\rho 并取对数可以得到

12ln⁡Eρ=52ln⁡R−ln⁡t\frac{1}{2}\ln \frac{E}{\rho} = \frac{5}{2}\ln R - \ln t \\

或

52ln⁡R=ln⁡t+12ln⁡Eρ\frac{5}{2}\ln R = \ln t + \frac{1}{2}\ln \frac{E}{\rho} \\

结果

三位一体原子弹

根据以上模型得到的公式，我们可以根据原子弹爆炸后某时刻的冲击波半径来估算原子弹爆炸释放的能量。图 4 是原子弹爆炸后 t=25t=25毫秒后产生的冲击波照片。照片已经根据原比例尺缩放到等比例的坐标系中。通过计算可以得出冲击波的半径大约为 130 m。空气的密度为 1.2kg/m3\rm kg/m^3，代入模型公式，可以得到原子弹爆炸产生的能量 EE 约为 7.1×10137.1×10^{13} J，这一能量相当于 1.7 万吨 TNT。这个简单的计算得到的结果同官方公开的数据（两万吨 TNT）相差仅 15%。

此外，我们还可以对 ln⁡t\ln t 和 5/2ln⁡R5/2\ln R 进行线性拟合。拟合需要原子弹爆炸不同时刻的冲击波半径，这些数据可以在文献 [4]中找到（见附录）。拟合出的直线如图 5 所示。

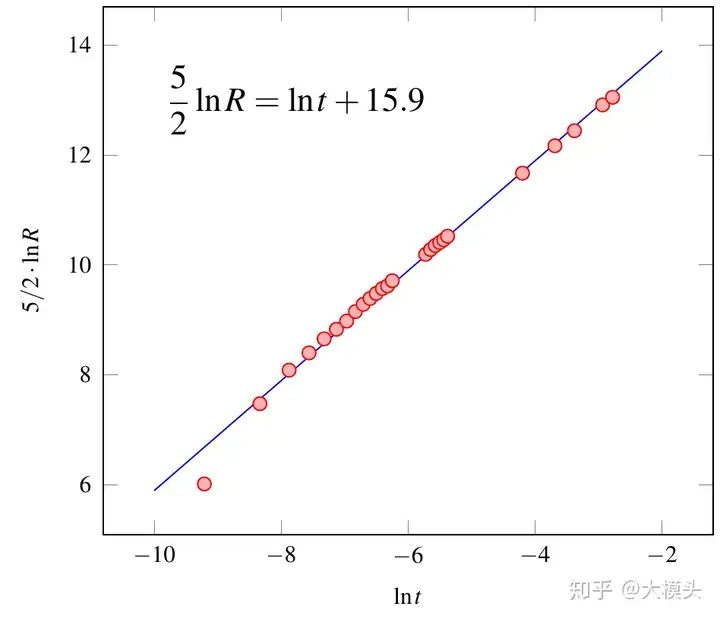
结果显示 ln⁡t\ln t 与 5/2ln⁡R5/2\ln R 呈现非常好的线性关系，这也再一次验证了模型的正确性。拟合还得到了直线在纵坐标轴上的截距：

12ln⁡Eρ=15.9\frac{1}{2}\ln \frac{E}{\rho} = 15.9 \\

代入空气的密度，可得原子弹爆炸释放的能量为

E=ρ⋅e15.9×2=7.76×1013JE = \rho\cdot \mathrm{e}^{15.9\times 2} = 7.76\times 10^{13}\,\mathrm{J} \\

这相当于 1.8 万吨 TNT。通过拟合得到的结果同官方公开的数据（二万吨 TNT）相差仅 10%。

贝鲁特港硝酸铵

为了应用前文的模型计算贝鲁特港硝酸铵的爆炸当量，需要知道爆炸后时间与冲击波半径的数据。我们对图 1 视频中爆炸瞬间的六帧图像进行了提取，并对图像中的爆炸冲击波半径进行了估计，具体如图 6，图中的长度单位是像素。

最接近爆炸中心的建筑物是贝鲁特港口的谷仓（左侧白色建筑物）。通过 Google earth 可以估计出该谷仓的长度L=130±30L=130\pm 30 米，并根据该谷仓炸毁前的照片可估计出该谷仓的长高比 L/H=2.6L/H=2.6，从而最终估算出该谷仓高约H=130/2.6=50H=130/2.6=50 米（图 7）。

该谷仓在图 6a 中约占据 75 个像素，因此爆炸点附近的一个像素表示的实际长度约为 50/75=2/350/75=2/3 米。由此可估算出图 6 中各帧图像的冲击波半径，例如在第 2 帧图像（图 6b）中，冲击波的半径约为 120 个像素，对应的实际长度约为 120×2/3=80120\times 2/3= 80 米。

图 6 中相邻图像的时间间隔可由视频帧率来计算。该视频是由手机所拍，其帧率为 30 帧/秒，因此相邻帧的时间间隔为1/301/30 秒。以第一帧图像（图 6a）为 0 时刻，我们得到了一组不同时刻 tt的冲击波半径RR。假设第一帧图像对应着爆炸发生后 t0t_0（

拟合得到 t0=0.0154t_0=0.0154，这表明第一帧图像对应的时间是爆炸后 0.0154 s。同时还得到了(E/ρ)1/5=259.4767(E/\rho)^{1/5}=259.4767，因此可以估算出爆炸释放的能量：

E=259.47675×1.2=1.4115×1012JE = 259.4767^5\times 1.2 = 1.4115\times 10^{12}~\mathrm{J} \\

这相当于约 340 吨 TNT。荷兰特文特大学 Sander 博士也做了类似的计算，其给出的计算结果仅为 100 吨左右 [5]。而推特上的网友 Sina 通过计算给出的结果则高达 3000 吨 [6]。

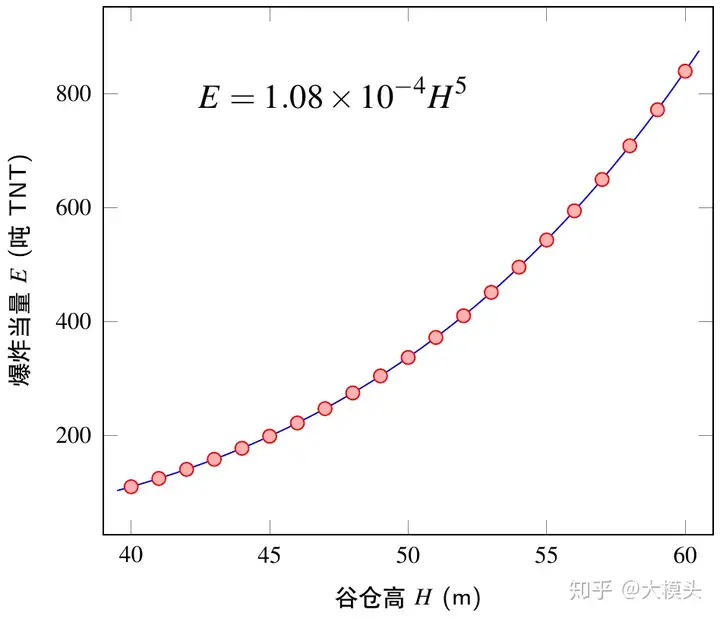
以上能量的计算依赖于谷仓高度的估计，该估计是不确定性的最大来源。而由此确定的冲击波半径又极大地影响能量的计算（五次方），因此谷仓高度的估计是能量计算误差的主要来源。考虑谷仓高度的不确定性为±10\pm 10米，即其高度在 40 至 60 米之间。重新应用上述过程进行计算，给出的爆炸当量在 110 至 840 吨（图 9）。

结论

量纲分析（点源爆炸模型）能够有效地估计出原子弹爆炸所释放的能量。1945 年美国的科学家在新墨西哥州阿拉莫戈多沙漠进行的三位一体核试验的当量约为 2 万吨。通过量纲分析得到的原子弹爆炸当量与官方公布的数据仅相差 10%。本文根据点源爆炸模型估算出贝鲁特港口大爆炸的当量为 340 吨。考虑估算中的误差，当量的不确定性范围为 110 至 840 吨。

附录

点击以下公众号文章左下角“阅读原文”获取本文 PDF 版和附件。

参考资料

[1] Wikipedia contributors. 2020 beirut explosions — Wikipedia, the free encyclopedia, 2020.:https://en.wikipedia.org/wiki/2020_Beirut_explosions

[2] Wikipedia contributors. Nuclear weapon — Wikipedia, the free encyclopedia, 2020.:https://en.wikipedia.org/wiki/Nuclear_weapon

[3] Wikipedia contributors. Nuclear weapon yield — Wikipedia, the free encyclopedia, 2020.:https://en.wikipedia.org/wiki/Nuclear_weapon_yield

[4] Geoffrey Ingram Taylor. The formation of a blast wave by a very intense explosion. ii. the atomic explosion of 1945. Proceedings of The Royal Society A: Mathematical, Physical and Engineering Sciences, 201(1065):175–186, 1950.

[5] Sander Huisman. Estimation of energy yield of 2020 beirut port explosion, 2020.:https://community.wolfram.com/groups/-/m/t/2051264

[6] Sina Booeshaghi. Using dimensional analysis i estimate that the energy contained in the awful, 2020.:https://twitter.com/sinabooeshaghi/status/1290727092884299778