制服无穷小-从阿基米德几何到牛顿二项式（三）

 

§4. 无限细分法的重要发现-Cavalieri

§4.1 一个似乎显而易见的原理

图4.1-1

Bonaventura Cavalieri的启蒙老师是Castelli，Cavalieri坚守Castelli的信条“数学才能有效疗愈堕落”，Castelli是如此喜欢自己这位学生，就把Cavalieri推荐给了自己的老师伽利略。Cavalieri 杰出的贡献在于提出了Cavalieris Prinple并借助代数方法推出y=axky=ax^k曲线的围合面积，1629年伽利略曾说：“Cavalieri是阿基米德之后在钻研几何学的深度和广度方面绝无仅有的人。”他的不可分量在后来牛顿的瞬时概念和莱布尼茨的微分概念中都有所反映，因此，Cavalieris Prinple是通向无穷小和微积分学的阶梯。其原理简述如下：

夹在两条平行直线之间的两个平面图形，被平行于这两条直线的任意直线所截，如果所得的两条截线长度相等，那么这两个平面图形的面积相等；夹在两个平行平面之间的两个立体图形，被平行于这两个平面的任意平面所截，如果所得的两个截面的面积相等，那么这两个立体图形的体积相等。通过以下几个图就会明白这个原理。

图4.1-2

图4.1-2中两摞硬币（同样币值和个数），虽然他们叠起的方式不同，但直觉上一下子就可以观察到，他们所占有的体积一样。

图4.1-3

图4.1-3中左边的多凌锥和右边的三菱锥高度一致，如果平行于底面的截面与多凌锥和三角锥所有截面积都相等，则两个棱锥的体积相等。

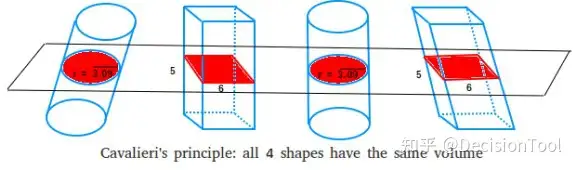
图4.1-4

图4.1-4中四个柱体的体积相同。

求面积也是同样道理，见图4.1-5，不用多解释。

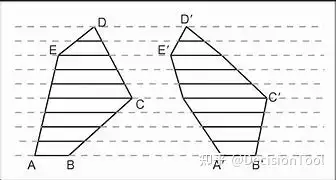
图4.1-5

Cavalieris Principle是一个直觉，但其不可分原理由于缺乏逻辑上的严密性，引起同时代一些数学家的异议。但他的原理给出了计算面积和体积的有效方法，其严格的数学定义甚至在牛顿时代也未完成，但正是这种不可分求和的思维方法造就了尔后的定积分概念的雏形。

从Cavalieris Principle可以有一个推论，同样也是很直觉，是对长度（面积）不同但比例相同，其面积（体积）之比也成比例。

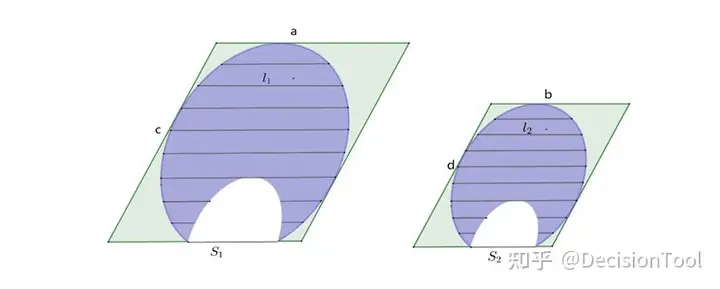
图4.1-6

如图4.1-6为两个平行四边形各内接一个不规则图形（即打横线的紫色部分），左边的图形与右边的图形，不仅其外接平行四边形各个边长之比相同，其等比例之处割线l1l_1与 l2l_2 之比也同样比例，即

l1l2=ab=cd\frac{l_1}{l_2}=\frac{a}{b}=\frac{c}{d} （式4.1-1）

左边图形紫色阴影部分面积 S1S_1，即平行于四边形边的割线从 l1l_1 一边滑向另外一边积累形成的图形面积，我们用符号 Σl1\Sigma{l_1} 来表示。同理，右边图形紫色阴影部分面积 S2S_2 用符号 Σl2\Sigma{l_2} 来表示，则有

S1S2=Σl1Σl2=acbd=a2b2=(l1l2)2\frac{S_1}{S_2}=\frac{\Sigma l_1}{\Sigma l_2}=\frac{ac}{bd}=\frac{a^{2}}{b^{2}}=(\frac{l_1}{l_2})^{2} （式4.1-2）

如果分别以S1S_1 和 S2S_2为底面积，作高分别为e 和f 的柱体或椎体（体积分别为 V1V_1 和 V2V_2 ），而且

ab=cd=ef\frac{a}{b}=\frac{c}{d}=\frac{e}{f}

则有

V1V2=ΣS1ΣS2=ΣacΣbd=Σl12Σl22=acebdf=a3b3=(l1l2)3\frac{V_1}{V_2}=\frac{\Sigma S_1}{\Sigma S_2}=\frac{\Sigma ac}{\Sigma bd}=\frac{\Sigma {l_1}^{2}}{\Sigma{l_2}^{2}}=\frac{ace}{bdf}=\frac{a^{3}}{b^{3}}=(\frac{l_1}{l_2})^{3} （式4.1-3）

对于（式4.1-1）到（式4.1-3）的推导是从直觉的角度，从数学证明的角度不够严密，有些别扭，这个推论对于后续的推理是起点。

但对于求高次方曲线的面积，仅仅是这个原理还不够，还需要代数（Algebra）方法的助力。这有别于古希腊的阿基米德时代，那时阿基米德手中还没有代数这个强大工具，只有圆规和直尺这两样工具，即使史上最伟大的天才，阿基米德也无力解决复杂的高次方函数面积计算。

§4.2 抛物线围合面积的计算

Cavalieri首先计算抛物线围合面积，他从一个正方形如图4.2-1开始。线段EF平分正方形ABCD并与对角线BD相交于M。虚线HK从AB开始向CD滑动，而且始终平行于AB，并与EF和BD分别相交于I和J。

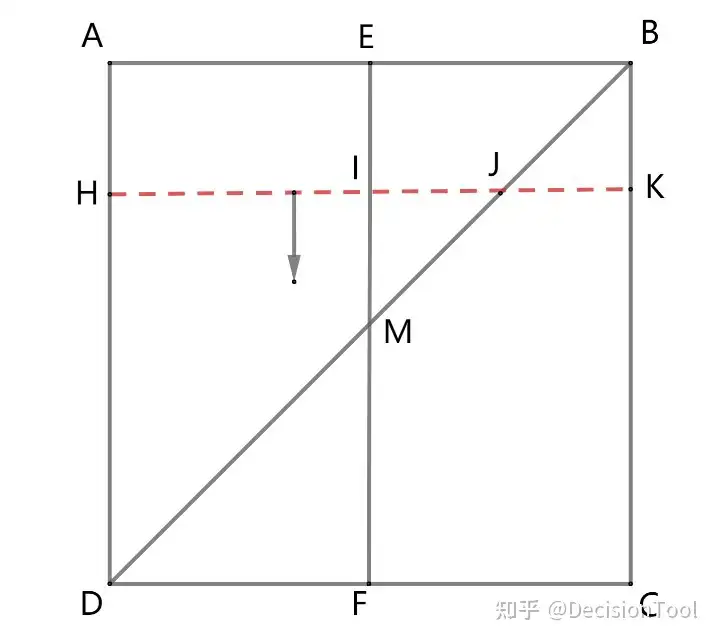
图4.2-1

Cavalieri设想作一正方形HJPQ，如图4.2-2，正方形HJPQ以HJ为边并垂直于正方形ABCD所在平面。当HK从AB滑向CD，以HJ为边的正方形面积不断变小，并且最终在点D消失为零。正方形HJPQ从平面ABRS滑向点D形成了一个四凌锥，其底面为ABRS顶点为D。为方便起见，这个四凌锥以符号△代表。

图4.2-2

取图4.2-1中的边长AD为轴，Cavalieri作图4.2-3，其中DH长度为，HN长度为，当图4.2-2中正方形HJPQ从ABRS滑向点D时，图4.2-3中的线段NH（NH的长度值为HIPQ的面积值）从线段LA向点D画出一条曲线LD。不难看出，曲线LD是抛物线。

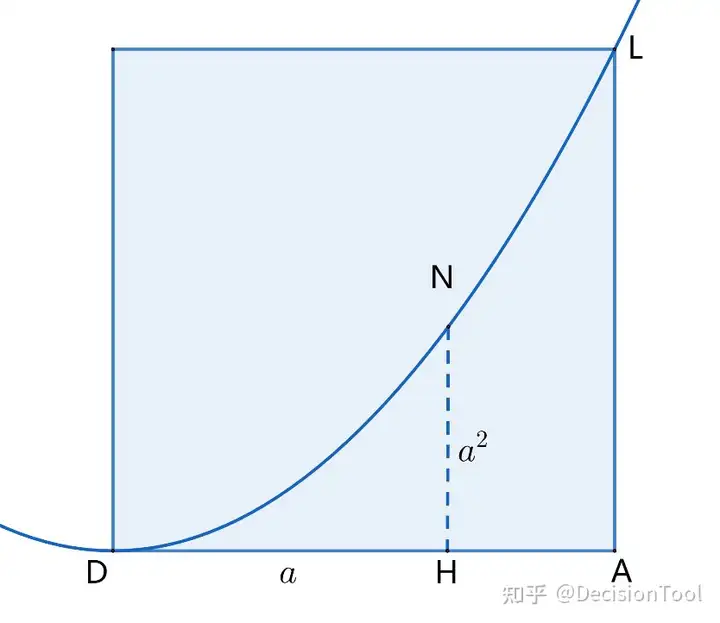
图4.2-3

按照Cavalieri 不可分割量组成面积（体积）的设想， △的体积值 V△V_△等同于抛物线DL与正方形边长DA围成的DAL的面积值SDALS_{DAL} 。

我们应该为这样的有创意的空间有趣联系喝彩，因为这样一来，如果知道了△的体积，也就知道了 SDALS_{DAL}。

图4.2-4

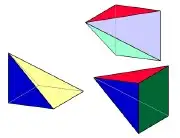
图4.2-5

图4.2-4和图4.2-5我们应该不陌生，一个正方体可以被分解为三个完全相同的四棱锥，其底面积为立方体的一个面的面积。所以

SDAL=13V△S_{DAL}=\frac{1}{3}V_△

但用视觉的物理的几何特征来推导曲线的围合面积，这可不是Cavalieri的目的，因为这样不能推广到一般情况，他引入代数符号另辟蹊径来解决这个问题。 这需要引入符号来表达，如在图4.2-2中，HJ是一个从长AB不断变小至点D（零）的变量，对于“所有以HJ为边长的正方形面积之和”， 用

∑ABD(HJ)2\sum_{AB}^{D}{(HJ)^2}

来表达，求和符号∑上下的符号AB和D表示以HJ为边正方形所滑过的范围。用这种符号表达，Cavalieri要用非几何方法证明

∑ABD(HJ)2=13∑ABD(AB)2\sum_{AB}^{D}{(HJ)^2}=\frac{1}{3}\sum_{AB}^{D}{(AB)^2} (式4.2-1）

图4.2-1中，有

(AB)2=(HJ+JK)2=(HJ)2+2(HJ⋅JK)+(JK)2(AB)^2=(HJ+JK)^2=(HJ)^2+2(HJ\cdot JK)+(JK)^2 (式4.2-2）

请注意这里的处理是关键，观察图4.2-1有,则有IJ=HJ−HIIJ=HJ-HI ,则有

IJ=HJ−IK,IJ=IK−JKIJ=HJ-IK, IJ=IK-JK

从而得出 2(IJ)=HJ−JK2(IJ)=HJ-JK,两边平方，得出

4(IJ)2=(HJ−JK)2=(HJ)2−2(HJ⋅JK)+(JK)24(IJ)^2=(HJ-JK)^2=(HJ)^2-2(HJ\cdot JK)+(JK)^2

从而有

2(HJ⋅JK)=(HJ)2+(JK)2−4(IJ)22(HJ\cdot JK)=(HJ)^2+(JK)^2-4(IJ)^2 (式4.2-3）

把（式4.2-3）代入（式4.2-2）可得

(AB)2=2(HJ)2+2(JK)2−4(IJ)2(AB)^2=2(HJ)^2+2(JK)^2-4(IJ)^2 (式4.2-4）

由于（式4.2-4）适用于任何线段HK，Cavalieri推断所有的正方形都将遵循这一规律，从而有

∑ABD(AB)2=2∑ABD(HJ)2+2∑BCD(JK)2−4∑EBDF(IJ)2\sum_{AB}^{D}{(AB)^2}=2\sum_{AB}^{D}{(HJ)^2}+2\sum_{B}^{CD}{(JK)^2}-4\sum_{EB}^{DF}{(IJ)^2} (式4.2-5）

观察图4.2-1，JK从DC滑向点B等同于HJ从AB滑向点D，我们有

∑ABD(HJ)2=∑DCB(JK)2\sum_{AB}^{D}{(HJ)^2}=\sum_{DC}^{B}{(JK)^2} (式4.2-6）

类似的

∑EBDF(IJ)2=2∑EBM(IJ)2\sum_{EB}^{DF}{(IJ)^2}=2\sum_{EB}^{M}{(IJ)^2} (式4.2-7）

在图4.2-2中，注意到三角形EBM与三角形ABD边长成比例 （1：2），由（式4.1-3）可得

∑ABD(HJ)2=8∑EBM(IJ)2\sum_{AB}^{D}{(HJ)^2}=8\sum_{EB}^{M}{(IJ)^2} (式4.2-8）

由（式4.2-7）和（式4.2-8）可得

∑ABD(HJ)2=4∑EBDF(IJ)2\sum_{AB}^{D}{(HJ)^2}=4\sum_{EB}^{DF}{(IJ)^2} (式4.2-9）

将（式4.2-9）和（式4.2-6）代入（式4.2-5）中得

∑ABD(AB)2=2∑ABD(HJ)2+2∑ABD(HJ)2−∑ABD(HJ)2=3∑ABD(HJ)2\sum_{AB}^{D}{(AB)^2}=2\sum_{AB}^{D}{(HJ)^2}+2\sum_{AB}^{D}{(HJ)^2}-\sum_{AB}^{D}{(HJ)^2}=3\sum_{AB}^{D}{(HJ)^2}

从而可得（式4.2-1），其表示抛物线围合面积为正方形面积的1/3。

注意，由（式4.1-3）推出（式4.1-8）是关键，这来自一个不严格的直觉数据关系，这里一定要注意相似的图形必须在边界的各个方向的长度比率都相同，否则是没有那种数值关系的。

在Cavalieri时代，还没有坐标系这种工具，求围合面积实际上是求出与外接的一个正方形面积的比率。

§4.3 一般曲线的围合面积

在系统地求解曲线围合面积（旋转体积）的过程中，“线段长度的幂次方”这个概念发挥了重要的作用。

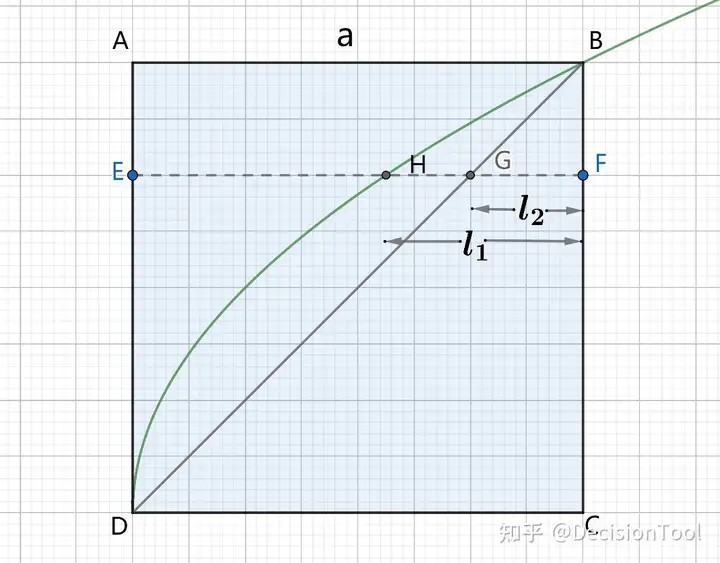
图4.3-1

一般地，假设任意一条曲线DHB，如图4.3-1，曲线DHB内接于边长为a的正方形ABCD，作平行于AB的线段EF，与曲线相交于点H，并与正方形对角线BD相交于点G，设HF=l1l_1，GF= l2l_2，曲线BHD与边BC和CD围合的面积用表示，正方形面积用表示，按照§4.1中Cavalieris Principle，可以表达为

SCBHDSCBAD=Σl1Σl2\frac{S_{CBHD}}{S_{CBAD}}=\frac{\Sigma l_1}{\Sigma l_2}

对于曲线DHB，可以一般地用l2l_2 的幂次方来表达 l1l_1 ，即 l1=f(l2)l_1=f(l_2)，则

SCBHDSCBAD=Σl1Σl2=Σf(l2)Σl2\frac{S_{CBHD}}{S_{CBAD}}=\frac{\Sigma l_1}{\Sigma l_2}=\frac{\Sigma f(l_2)}{\Sigma l_2}

则曲线围合面积 SCBHDS_{CBHD} 可以用三角形BDC的线段长度 l1l_1的幂次方的和来表达。围合面积SCBHDS_{CBHD} 以BC为轴旋转形成的柱体的体积 VBHDCV_{BHDC} ，与正方形面积以BC为轴旋转形成的圆柱体的体积 VABCDV_{ABCD} 之比为

VBHDCVABCD=Σl12Σa2=Σ[f(l2)]2Σa2\frac{V_{BHDC}}{V_{ABCD}}=\frac{\Sigma {l_1}^2}{\Sigma a^2}=\frac{\Sigma [f(l_2)]^2}{\Sigma a^2}

对于更一般情况，曲线表达为

ya=(xb)n\frac{y}{a}=(\frac{x}{b})^{n}

其中HF=y，BF=x，AD=b，AB=a，（即以B为原点，BC为x轴，BA为y轴），其与正方形的两个临边围合面积为

SCBHDSCBAD=Σl1Σa=ΣyΣa\frac{S_{CBHD}}{S_{CBAD}}=\frac{\Sigma l_1}{\Sigma a}=\frac{\Sigma y}{\Sigma a}

由于

l1a=(xb)n\frac{l_1}{a}=(\frac{x}{b})^{n}

并且

l2a=xb\frac{l_2}{a}=\frac{x}{b}

那么

l1a=(l2a)n\frac{l_1}{a}=(\frac{l_2}{a})^{n}

从而有

SCBHDSCBAD=Σl1Σa=Σl2nΣan\frac{S_{CBHD}}{S_{CBAD}}=\frac{\Sigma l_1}{\Sigma a}=\frac{\Sigma {l_2}^n}{\Sigma a^n}

对于体积比率则有

VBHDCVABCD=Σl12Σa2=Σl22nΣa2n\frac{V_{BHDC}}{V_{ABCD}}=\frac{\Sigma {l_1}^2}{\Sigma a^2}=\frac{\Sigma {l_2}^{2n}}{\Sigma a^{2n}}

所以求一般曲线面积和一般曲面旋转体体积的计算，变为对于三角形平行于底边分割线幂次方的求和，如图4.3-2，分割线EG=ll 平行于三角形ABD底边AB，对 ll 或 l2l^2 的求和， Σl\Sigma l 或 Σl2\Sigma l^2 ，

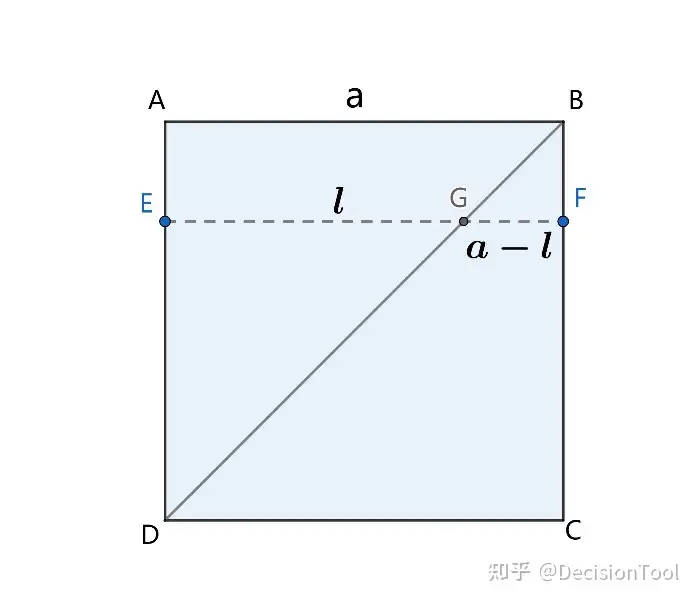
图4.3-2

Cavalieri计算出了椭圆、抛物线、双曲线、棱锥、圆锥等各种曲线的面积和体积，成功地计算出

ΣlΣa=12,Σl2Σa2=13,Σl3Σa3=14,Σl4Σa4=15,Σl5Σa5=16\frac{\Sigma l}{\Sigma a}=\frac{1}{2}, \frac{\Sigma {l}^2}{\Sigma a^2}=\frac{1}{3}, \frac{\Sigma {l}^3}{\Sigma a^3}=\frac{1}{4}, \frac{\Sigma {l}^4}{\Sigma a^4}=\frac{1}{5}, \frac{\Sigma {l}^5}{\Sigma a^5}=\frac{1}{6}

Cavalieri据此外推而得，对于正整数n，下式成立

\frac{\Sigma {l}^n}{\Sigma a^n}=\frac{1}{n+1}

下面以\frac{\Sigma {l}^5}{\Sigma a^5}=\frac{1}{6} 为例，看看Cavalieri如何巧妙地利用代数来推导。

§4.4 代数运算的决定性作用

代数（Algebra）原创于阿拉伯地区，这在Alhazen的方法里面就有所体现，Cavalieri的几何方法借助于代数的运算能力，才将更一般性的曲线面积求解。

图4.4-1

作图4.4-1，正方形ACGQ被对角线分为两个全等的三角形ACQ和CQD，BN和DH将ACGQ等分为四个全等的正方形ABMD、BCHM、DMQN和MHGN，并与对角线CQ相交于M。作与DH平行且距离相等的线段RV和R{}V{}，为了推导方便，令

RS=S{}V{}=a, ST=S{}T{}=b

则有 TV=T{}R{}=a-b

借助于代数公式 (a+b)^5+(a-b)^5=2a^5+20a^3 b^2+10ab^4

对于矩形ACHD，我们有

\sum_{AC}^{DM}{(a+b)^5}+\sum_{C}^{MH}{(a-b)^5}=2\sum_{AB}^{DM}{a^5}+20\sum_{BC}^{M}{a^3b^2}+10\sum_{BC}^{M}{ab^4} （式4.4-1）

类似地，对于矩形DHGQ有

\sum_{QG}^{MH}{(a+b)^5}+\sum_{Q}^{DM}{(a-b)^5}=2\sum_{NG}^{MH}{a^5}+20\sum_{QN}^{M}{a^3b^2}+10\sum_{QN}^{M}{ab^4} （式4.4-2）

将矩形ACHD和DHGQ相加，即（式4.4-1）和（式4.4-2）相加，同时注意到ABMD=MHGN和△BMC=△QMN，有

\sum_{AC}^{Q}{RT^5}+\sum_{QG}^{C}{TV^5}=2\sum_{AB}^{QN}{a^5}+40\sum_{BC}^{M}{a^3b^2}+20\sum_{BC}^{M}{ab^4} （式4.4-3）

这里要注意，a 作为一个常量，而b 作为一个变量，因为△ACQ=△CQG，则有

\sum_{AC}^{Q}{RT^5}=\sum_{QG}^{C}{TV^5}

从而有

\sum_{AC}^{Q}{RT^5}+\sum_{QG}^{C}{TV^5}=2\sum_{QG}^{C}{TV^5} （式4.4-4）

从§4.2节中证明的（式4.2-1）可知

\sum_{BC}^{M}{b^2}=\frac{1}{3}\sum_{BC}^{MH}{a^2}=\frac{1}{6}\sum_{BC}^{NG}{a^2} （式4.4-5）

同理，5次方之前的幂次方也都已经推出，即有

\sum_{BC}^{M}{b^4}=\frac{1}{5}\sum_{BC}^{MH}{a^4}=\frac{1}{10}\sum_{BC}^{NG}{a^4} （式4.4-6）

结合上述三式可得

\sum_{AC}^{Q}{RT^5}+\sum_{QG}^{C}{TV^5}=2\sum_{QG}^{C}{TV^5}=2\sum_{AB}^{QN}{a^5}+\frac{20}{3}\sum_{BC}^{GN}{a^5}+2\sum_{BC}^{GN}{a^5} =\frac{32}{3}\sum_{AB}^{QN}{a^5} =\frac{1}{3}\sum_{AC}^{QG}{AC^5}

（式4.4-7）

因为 AC=2a，AC^5=32a^5 ，最后得到

\sum_{AC}^{Q}{RT^5}=\frac{1}{6}\sum_{AC}^{QG}{AC^5} （式4.4-8）

注意，任何高次幂的求和，都会用到所有低次幂的结果，这是一个递归过程。例如在求5次幂的过程中，4, 3, 2次幂的结果一般都会在计算过程中用到。

Cavalieri成功地计算出从2次一直到9次幂函数的围合面积，发现了一般规律，并推断，用现代的积分符号表示出来，即是

∫_0^1x^k dx=\frac{1}{k+1} （式4.4-9）

并且利用反函数，即 y=x^k 等效于 x=\sqrt[k]{y} ，从而计算出函数 y=\sqrt[k]{x}的围合面积（与y=x^k 在单位正方形内互补）为

1-\frac{1}{k+1}=\frac{k}{k+1}

用现代的积分符号表示出来，即是

∫_0^1\sqrt[k]{x} dx=1-\frac{1}{k+1}=\frac{k}{k+1}