神经网络的函数逼近是什么意思?
从数学的角度来说,就是拟合一个输入变量到输出变量的函数关系 ff 。
在某些情况下,由于数据比较复杂,数据维度高,输入输出之间的函数关系 ff比较复杂,我们无法精确地把这个函数“写出来”,但是我们可以通过寻找输入变量与输出变量的关系来将整个函数“拟合出来”,这个拟合的过程就是逼近的过程。
拟合完成以后,我们得到一个神经网络模型 gg ,使得 loss(f,g)≤δloss(f, g) \leq \delta,当然,δ\delta 是我们自己设定的一个数值,小于这个值表示我们觉得 ff 和 gg 已经非常接近了,几乎可以认为他们是一个函数。而这个 loss()loss() 就是我们的损失函数,通常用MSE,RMSE等方法来构造。
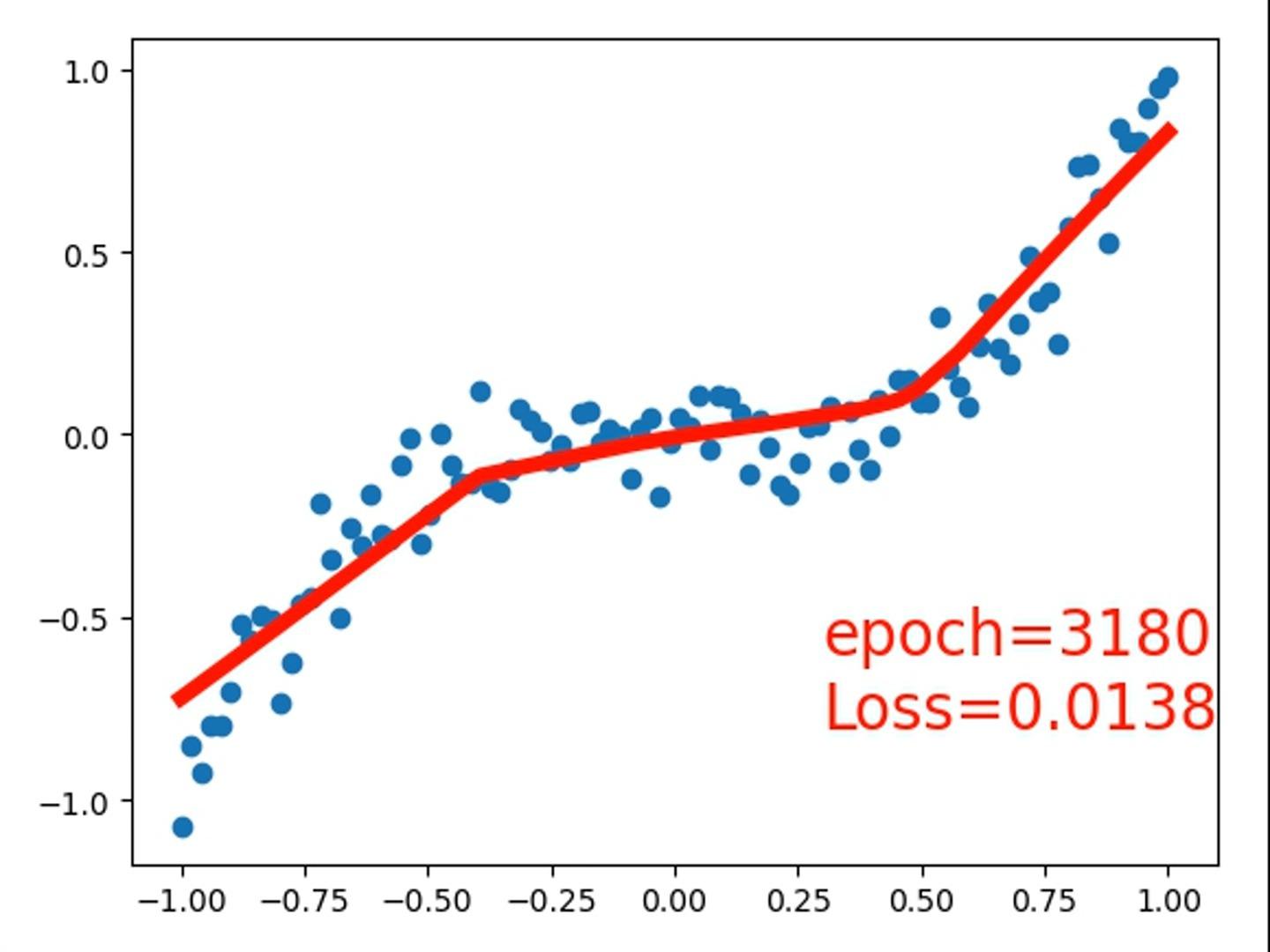
用一个简单的视频来演示神经网络“逼近”的过程,视频中采用的是一个具有2个神经网络层,每层32个神经元的全连接网络来拟合我们的“目标函数”。耐心看完哦!
使用了Pytorch框架,代码在这里:
#-*-coding:UTF-8 -*-
import torch
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
from torch.autograd import Variable
#%% 构造数据
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # 100 x 1 的数据
y = x.pow(3) + 0.1 * torch.randn(x.size())
x, y = (Variable(x), Variable(y))
plt.scatter(x, y)
plt.scatter(x.data, y.data)
plt.scatter(x.data.numpy(), y.data.numpy())
plt.ion() # 打开交互模式,绘制图片以后不会卡在plt.show()那条语句那里
plt.show()
#%% 定义具有2个隐藏层的全连接前馈神经网络类
class Net1(nn.Module):
def __init__(self, n_input, n_hidden, n_output):
super(Net1, self).__init__()
self.hidden_1 = nn.Linear(n_input, n_hidden)
self.hidden_2 = nn.Linear(n_hidden, n_hidden)
self.predict = nn.Linear(n_hidden, n_output)
def forward(self, input):
out = self.hidden_1(input)
out = F.relu(out)
out = self.hidden_2(out)
out = F.sigmoid(out)
out = self.predict(out)
return out
#%% 使用Sequential方法定义具有2个隐藏层的全连接前馈神经网络类
class Net2(nn.Module):
def __init__(self, n_input, n_hidden, n_output):
super().__init__()
self.layer = nn.Sequential(
nn.Linear(n_input, n_hidden),
nn.ReLU(True), # 使用ReLU作为第1个隐藏层的激活函数, 设定为True表示将输出直接赋给输入,目的是节约内存
nn.Linear(n_hidden, n_hidden),
nn.Sigmoid(), # 使用Sigmoid作为第2个隐藏层的激活函数
nn.Linear(n_hidden, n_output)
)
def forward(self, input):
return self.layer(input)
#%% 使用Sequential方法定义具有2个隐藏层的全连接前馈神经网络类
class Net3(nn.Module):
def __init__(self, n_input, n_hidden, n_output):
super().__init__()
self.layer = nn.Sequential()
self.layer.add_module(input_layer, nn.Linear(n_input, n_hidden))
self.layer.add_module(relu_func, nn.ReLU()) # 使用ReLU作为第1个隐藏层的激活函数
self.layer.add_module(hidden_layer_2, nn.Linear(n_hidden, n_hidden))
self.layer.add_module(sigmoid_func, nn.Sigmoid()) # 使用Sigmoid作为第2个隐藏层的激活函数
self.layer.add_module(output_layer, nn.Linear(n_hidden, n_output))
def forward(self, input):
return self.layer(input)
#%% 构造网络实体
n_input = 1
n_hidden = 32
n_output = 1
# 两种构造网络的方法
# net = Net1(n_input, n_hidden, n_output)
# net = Net2(n_input, n_hidden, n_output)
net = Net3(n_input, n_hidden, n_output)
print(net)
# 采用SGD作为优化方法, MSE作为loss
optimizer = torch.optim.SGD(net.parameters(), lr=0.05) # 设置学习速率为0.1
loss_func = torch.nn.MSELoss()
for t in range(4000):
prediction = net(x)
loss = loss_func(prediction, y) # 计算loss,这里为MSE
# 把梯度置零
optimizer.zero_grad()
# 误差反向传播,计算参数更新值
loss.backward()
# 更新参数
optimizer.step()
if t%5 == 0:
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), r-, lw=5)
plt.text(0.3, -0.6, epoch=%d % t, fontdict={size: 20, color: red})
plt.text(0.3, -0.8, Loss=%.4f % loss.data, fontdict={size: 20, color: red})
plt.pause(0.05)
plt.ioff() # 关闭交互模式
plt.show()
本站所有文章、数据、图片均来自互联网,一切版权均归源网站或源作者所有。
如果侵犯了你的权益请来信告知我们删除。邮箱:dacesmiling@qq.com