一个初步的斯托克斯定理的证明

 

一、涉及的矢量叉乘的知识

分配律：

u→×(v→+w→)=u→×v→+u→×w→(v→+w→)×u→=v→×u→+w→×u→\overrightarrow{u}\times\left( \overrightarrow{v}+\overrightarrow{w}\right)=\overrightarrow{u}\times \overrightarrow{v}+\overrightarrow{u}\times \overrightarrow{w}\\\left(\overrightarrow{v}+\overrightarrow{w} \right)\times\overrightarrow{u}=\overrightarrow{v}\times\overrightarrow{u}+\overrightarrow{w}\times\overrightarrow{u}

坐标运算：在笛卡尔坐标系中，假定

u→=u1i→+u2j→+u3k→v→=v1i→+v2j→+v3k→\overrightarrow{u}=u_1\overrightarrow{i}+u_2\overrightarrow{j}+u_3\overrightarrow{k }\\\overrightarrow{v}=v_1\overrightarrow{i}+v_2\overrightarrow{j}+v_3\overrightarrow{k }

由分配律有

u→×v→=(u1i→+u2j→+u3k→)×(v1i→+v2j→+v3k→)=u1v1i→×i→+u1v2i→×j→+u1v3i→×k→+u2v1j→×i→+u2v2j→×j→+u2v3j→×k→+u3v1k→×i→+u3v2k→×j→+u3v3k→×k→=u1v2k→−u1v3j→−u2v1k→+u2v3i→+u3v1j→−u3v2i→=(u2v3−u3v2)i→−(u1v3−u3v1)j→+(u1v2−u2v1)k→\overrightarrow{u}\times \overrightarrow{v}=\left(u_1\overrightarrow{i}+u_2\overrightarrow{j}+u_3\overrightarrow{k}\right)\times \left(v_1\overrightarrow{i}+v_2\overrightarrow{j}+v_3\overrightarrow{k}\right)=u_1 v_1\overrightarrow{i}\times \overrightarrow{i}+u_1v_2\overrightarrow{i}\times\overrightarrow{j}+u_1 v_3\overrightarrow{i}\times\overrightarrow{k}+u_2 v_1\overrightarrow{j}\times \overrightarrow{i}+u_2v_2\overrightarrow{j}\times\overrightarrow{j}+u_2 v_3\overrightarrow{j}\times\overrightarrow{k}+u_3 v_1\overrightarrow{k}\times \overrightarrow{i}+u_3v_2\overrightarrow{k}\times\overrightarrow{j}+u_3 v_3\overrightarrow{k}\times\overrightarrow{k}=u_1 v_2\overrightarrow{k}-u_1 v_3 \overrightarrow{j}-u_2 v_1\overrightarrow{k}+u_2v_3\overrightarrow{i}+u_3v_1\overrightarrow{j}-u_3v_2\overrightarrow{i}=\left(u_2v_3-u_3v_2\right)\overrightarrow{i}-\left(u_1v_3-u_3v_1\right)\overrightarrow{j}+\left(u_1v_2-u_2v_1\right)\overrightarrow{k}

新矢量 u→×v→\overrightarrow{u}\times \overrightarrow{v} 的分量式可以由此写出，即

(u→×v→)x=u2v3−u3v2(u→×v→)y=−(u1v3−u3v1)(u→×v→)z=u1v2−u2v1\left(\overrightarrow{u}\times \overrightarrow{v}\right)_x=u_2v_3-u_3v_2\\\left(\overrightarrow{u}\times \overrightarrow{v}\right)_y=-\left(u_1v_3-u_3v_1\right)\\\left(\overrightarrow{u}\times \overrightarrow{v}\right)_z=u_1v_2-u_2v_1

二、涉及的算符（operator） ∇\nabla 的知识

算符 ∇\nabla首先是一个微分算符（功能上），其次还是一个矢量算符（性质上），因为我们可以对它写分量式

∇x=∂∂x,∇y=∂∂y,∇z=∂∂z\nabla_x=\frac{\partial}{\partial x},\nabla_y=\frac{\partial}{\partial y},\nabla_z=\frac{\partial}{\partial z} 即 ∇=(∂∂x,∂∂y,∂∂z)\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)

我们必须记住 ∇\nabla 是一个算符，它只有和某个场（或者说某个函数）发生运算后才有意义。

现在就让我们用它来设计一种运算——让∇\nabla 通过叉乘对某个矢量场 h→(x,y,z)\overrightarrow{h}\left(x,y,z\right) 求某种微分，即 ∇×h→\nabla\times\overrightarrow{h}

有了前面的铺垫，我们可以轻松地写出这个新矢量的分量式，即

(∇→×h→)x=∇yhz−∇zhy=∂hz∂y−∂hy∂z(∇→×h→)y=−(∇xhz−∇zhx)=−(∂hz∂x−∂hx∂z)(∇→×h→)z=∇xhy−∇yhx=∂hy∂x−∂hx∂y\left(\overrightarrow{\nabla}\times \overrightarrow{h}\right)_x=\nabla_yh_z-\nabla_zh_y=\frac{\partial h_z}{\partial y}-\frac{\partial h_y}{\partial z}\\\left(\overrightarrow{\nabla}\times \overrightarrow{h}\right)_y=-\left(\nabla_xh_z-\nabla_zh_x\right)=-\left(\frac{\partial h_z}{\partial x}-\frac{\partial h_x}{\partial z}\right)\\\left(\overrightarrow{\nabla}\times \overrightarrow{h}\right)_z=\nabla_xh_y-\nabla_yh_x=\frac{\partial h_y}{\partial x}-\frac{\partial h_x}{\partial y}

这个新矢量 ∇×h→\nabla\times\overrightarrow{h} 称为 h→\overrightarrow{h}的旋度，不过这是后话了。

三、斯托克斯定理的证明

斯托克斯定理的表述：某个矢量绕某个回路的环流等于该矢量的旋度的法向分量对该回路围成的平面的面积分。即

∮C→⋅ds→=∫∫S(∇×C→)nda\oint_{}^{}\overrightarrow{C}\cdot d\overrightarrow{s}=\int_{}^{}\int_{S}^{}\left(\nabla\times\overrightarrow{C}\right)_nda

注意：1. ds→d\overrightarrow{s} 的方向由绕行方向决定， dada 表示面元的面积。

2.这里提到的“该矢量的旋度的法向分量”是讲究正负的，以回路绕行方向的右手螺旋拇指方向为正方向。

对于环流这里不再赘述。直接开证。

首先说明一个看似浅显却相当重要的结论。

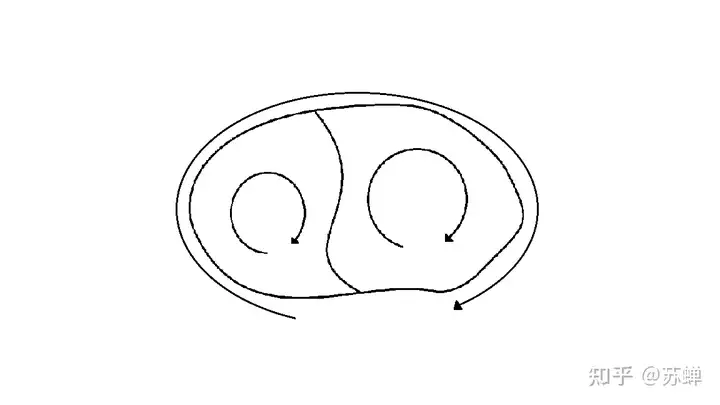
容易发现，如果采用相同的绕行方向，那么绕整个回路的环流等于绕两个分回路的环流之和。在此基础上，如果我们对分回路继续进行分割，便不难发现更一般的规律：如果采用相同的绕行方向，那么某个回路的环流等于它所有分回路的环流的总和。

有了这个规律，我们就可以放心大胆地用微元法进行尝试了，因为任何面都可以看作是由无数面元拼成的。

方便起见，我们让回路落在某个右手系的xOyxOy 平面内，并且使该回路的绕行方向的右手螺旋拇指方向（即法向）指向 zz 轴正方向。（实际上这些规定都不会影响结果的一般性，不过这也是后话了）

为了方便计算，我们将面元取成一个无限小的正方形

现在我们来计算一下这个回路的环流。

在不考虑修正的情况下，

∮C→⋅s→=CxΔx+CyΔy−CxΔx−CyΔy=0\oint_{}^{}\overrightarrow{C}\cdot \overrightarrow{s}=C_x\Delta x+C_y\Delta y-C_x\Delta x-C_y\Delta y=0

这对于一级近似是对的，然而，可以更精确一些。如果考虑 Cx,CyC_x,C_y 的变化率，便可以写出

∮C→⋅s→=CxΔx+(Cy+∂Cy∂xΔx)Δy−(Cx+∂Cx∂yΔy)Δx−CyΔy=(∂Cy∂x−∂Cx∂y)ΔxΔy=(∇×C→)zΔa\oint_{}^{}\overrightarrow{C}\cdot \overrightarrow{s}=C_x\Delta x+\left(C_y+\frac{\partial{C_y}}{\partial{x}}\Delta x\right)\Delta y-\left(C_x+\frac{\partial{C_x}}{\partial{y}}\Delta y\right)\Delta x-C_y\Delta y=\left(\frac{\partial{C_y}}{\partial{x}}-\frac{\partial{C_x}}{\partial{y}}\right)\Delta x\Delta y=\left(\nabla\times\overrightarrow{C}\right)_z \Delta a

这个 zz分量实际上就是该面元的法向分量。因此可以将绕一个无限小正方形的环流写成一种更一般的形式，即

∮C→⋅s→=(∇×C→)nΔa\oint_{}^{}\overrightarrow{C}\cdot \overrightarrow{s}=\left(\nabla\times\overrightarrow{C}\right)_n \Delta a

由此我们知道，某矢量 C→\overrightarrow{C} 绕一无限小正方形的环流，等于 C→\overrightarrow{C}在该面元处的旋度的法向分量乘以该正方形面积。

现在，我们可以将回路的环流和矢量场的旋度轻而易举地联系起来了，因为任何一个回路都可以看做是被一系列无限小正方形所填满的。把所有小正方形的环流叫起来，这个和可以写成一个积分，其结果便是上述的斯托克斯定理，即

∮C→⋅ds→=∫∫S(∇×C→)nda\oint_{}^{}\overrightarrow{C}\cdot d\overrightarrow{s}=\int_{}^{}\int_{S}^{}\left(\nabla\times\overrightarrow{C}\right)_nda

这种证明方法简洁明快，美中不足的是一处近似处理不是很完美，希望未来能够加以完善。