怎么区分不同的音色？

谢（不知道是谁）邀。

（这个问题其实邀请音乐方面的答主可能不好回答，最好是做物理或者信息方面的更适合回答。）

小学自然课程讲过：声音是由物体振动产生的。因此声音的任何性质都可以和振动与波动的物理性质进行关联。

乐音（有固定音高的音）有三要素，响度，音高和音色。他们在物理上分别对应了声波的振幅，频率还有【每个周期内的振动形式】（自己造的词，谁能告诉我物理上叫什么）。前两者很好理解，略过不谈。主要来说说第三个，也就是题主的问题。

有固定音高（频率）的乐音，都是周期函数。同样音量意味着振幅相同，同样音高意味着周期相同。但是这二者并不能完全确定一个周期函数。

下图中的三个函数都是振幅为1，周期为1的函数。

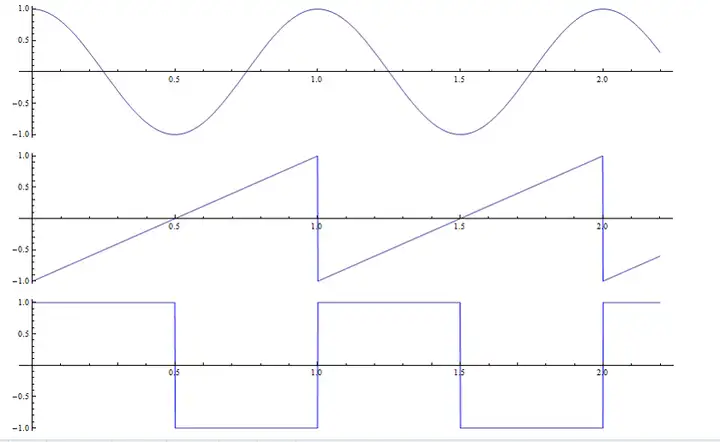
它们分别为正弦波、三角波、方波。如果将这三者转化成为振动，那么产生的声音就是同音量、同音高、不同音色的三个乐音。产生差别的是【每个周期内的振动形式】。

顺带一提的是，我们日常说话是带音高的，那么同样一个音高下说（或者唱）不同的元音（a o i）完全可以区分，也是利用的音色的不同。

解释一下其他答主提到的。

有几位答主提到说乐器的结构、材料不同，还有从物理上说振动的初始条件不同的，正是这些原因的不同导致了最终产生的振动的【每个周期内的振动形式】的不同。

另一个答主提到了频谱的不同，这个和我答案中的【每个周期内的振动形式】其实是一码事。解释起来稍微有点复杂，我试着慢慢说。

首先的一个概念叫做傅里叶分解，数学上告诉我们，任何一个周期为T的，满足Dirichlet条件的（别问我是什么）函数，都可以分解为三角函数级数求和。也就是 f(t)=a0+∑n=1∞[ansin⁡(nωt)+bncos⁡(nωt)]f(t)=a_0+\sum_{n=1}^{\infty}[a_n\sin(n\omega t)+b_n\cos(n\omega t)]

其中 ω=2π/T\omega=2\pi/T. 这从数学上说明了任何（正常的）周期振动都能够分解为三角振动的叠加，上图中的方波也可以分解为三角波。下面这个图中红线分别是采用了前1-4级展开的结果，可以发现它在收敛于黑色的方波信号。

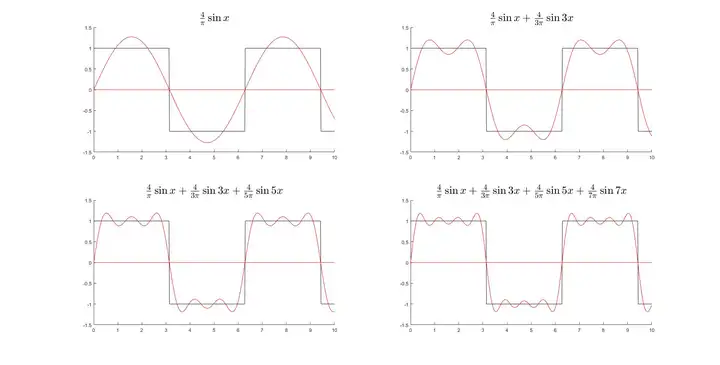
这是个无穷级数，项数越多越精确。不同的周期函数的三角函数展开，只有前面的系数是不一样的。

在这个基础上，三角函数展开之后系数和周期函数存在一一对应的关系。因此我们可以用前面的系数来表示周期函数。在上面的例子中，这个方波不仅仅可以用