为什么 30 个样本就称为「大样本」，而不是 40 或 50？

谢邀。我保证不打死写书的。

大样本理论是什么？n→∞n\rightarrow \infty，也就是样本量趋向于无穷的时候。30≈∞30\approx \infty?

究竟多少数据是大样本？这个真的很难说。

首先，你有多少个参数需要估计？我有29个参数，你只有30个样本，这也能叫大样本？实际情况是当你有29个参数的时候，你会过度拟合数据，而且得到的参数估计偏差很大。

其次，你用的什么统计方法？我猜数理统计书上这么写仅仅是针对特殊情况的特殊模型，暗含特殊假设吧？不同统计方法的收敛速度可能差别很大的，很多情况下可能根本不是n−consistent\sqrt{n}-consistent 的估计量。比如我做一个最简单的一元非参数回归，收敛速度可能是n4/5\sqrt{n^{4/5}} ，收敛速度可以看看图：

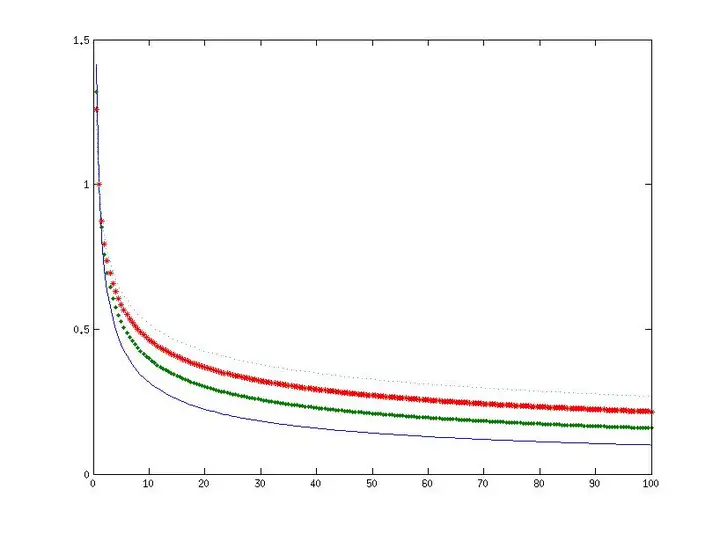
最下面，也就是收敛速度最快的是n\sqrt{n}，接下来分别是收敛速度可能是n4/5\sqrt{n^{4/5}}，n4/6\sqrt{n^{4/6}} 。。。分别代表着一维、二维、三维的非参数估计的收敛速度。你看看在n=30n=30这个点上差别有多大。

最后，就算你的数据是服从正态的，而且就是为了计算一个均值，我们来看，n(x¯−μ)∼N(0,σ2)\sqrt{n}\left( \bar{x} -\mu \right) \sim N\left( 0,\sigma^2\right) ，你是不是还要考虑数据的方差有多大啦？如果数据方差很大，为了达到某个精度，恐怕几百个样本都不够。当然，这还是数据服从正态所以你有精确的小样本特性的时候，非正态30个样本？呵呵了。

特别现在都大数据时代了，数据量还是问题？数据量不到100我是绝对不敢拿出来的，更何况我们做东西动辄几千几万的样本。

这个30有没有道理？我猜是没有道理的。

===========================

回应一下

t分布是一个很好的想法，但是这里并不能回避一个很严重的问题。

什么问题呢？首先我们得先来谈一下为什么我们需要大样本理论。因为在很多情况下，有限样本的统计量的分布我们是不知道的。正态分布是一个特例，在正态分布的情况下，我们可以得到样本均值的精确分布（得益于正态分布相加还是正态分布），进而得到假设检验时候的t分布。

但是！很多情况下，数据并不是正态分布的，比如，是卡方分布，那么小样本情况下我们很难得到其样本均值的精确分布，所以我们需要大样本理论，因为如果样本足够大，那么其均值渐进的服从正态分布（z值）。

这里你要注意，精确的t分布是一定要假设正态分布的，否则你上面不是正态，下边不是卡方，你还不能证明上面和下面独立，怎么能证明出是t分布呢？

而即使是在大样本下，大家发现做假设检验的时候对自由度进行惩罚一般来说检验统计量表现的更好，所以大家大样本条件下还是会用t分布。

所以这里个人感觉用t分布来说明30是大样本有点逻辑上的问题。本来大样本提出来是为了解决小样本非正态总体的情况下，精确分布不知道的问题，而t分布是在假设了正态之后才能精确的得出，所以两者前提条件都不一样，这样很难说服别人。

这里给大家举个栗子。我从χ2(3)\chi^2\left( 3 \right)抽出30个样本出来，计算均值，重复这个过程1000次，这样我就得到了这些均值的分布：

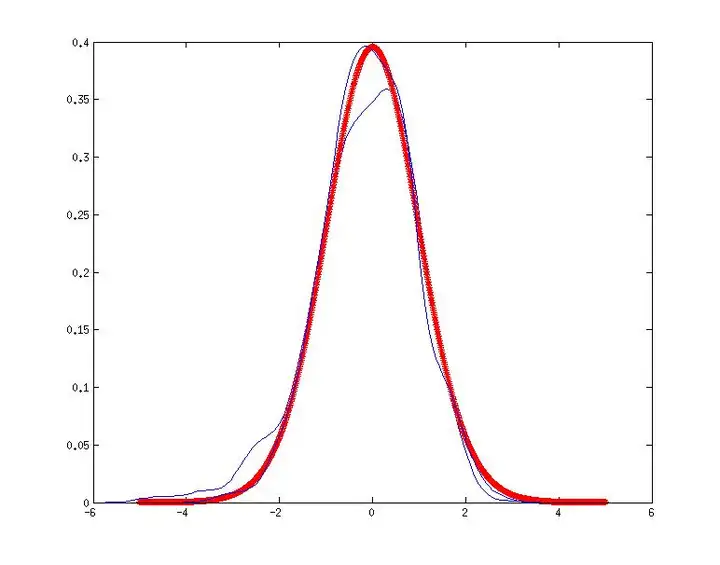
其中红色的是t(30)的概率密度函数，红色的中间夹着一条蓝色的线，是样本量为30的正态均值的分布，可见的确跟t分布是一样的。但是大家看下面那条蓝色的线，是样本量为30的卡方分布的均值的分布，是不是差别很大？你还敢说在非正态的条件下，30是大样本么？附Matlab Code: